【題目】已知函數
ae2x+(a﹣2) ex﹣x.
（1）討論
的單調性；
（2）若
有兩個零點，求a的取值范圍.
【答案】（1）見解析；（2）
.
【解析】試題分析：（1）討論
單調性，首先進行求導，發現式子特點后要及時進行因式分解，再對
按
， 
進行討論，寫出單調區間；（2）根據第（1）問，若
， 
至多有一個零點.若
，當
時， 
取得最小值，求出最小值
，根據
， 
， 
進行討論，可知當
時有2個零點.易知
在
有一個零點；設正整數
滿足
，則
.由于
，因此
在
有一個零點.從而可得
的取值范圍為
.
試題解析：（1）
的定義域為
， 
，
（ⅰ）若
，則
，所以
在
單調遞減.
（ⅱ）若
，則由
得
.
當
時， 
；當
時， 
，所以
在
單調遞減，在
單調遞增.
（2）（ⅰ）若
，由（1）知， 
至多有一個零點.
（ⅱ）若
，由（1）知，當
時， 
取得最小值，最小值為
.
①當
時，由于
，故
只有一個零點；
②當
時，由于
，即
，故
沒有零點；
③當
時， 
，即
.
又
，故
在
有一個零點.
設正整數
滿足
，則
.
由于
，因此
在
有一個零點.
綜上， 
的取值范圍為
.
點睛:研究函數零點問題常常與研究對應方程的實根問題相互轉化.已知函數
有2個零點求參數a的取值范圍，第一種方法是分離參數，構造不含參數的函數，研究其單調性、極值、最值，判斷
與其交點的個數，從而求出a的取值范圍；第二種方法是直接對含參函數進行研究，研究其單調性、極值、最值，注意點是若
有2個零點，且函數先減后增，則只需其最小值小于0，且后面還需驗證最小值兩邊存在大于0的點.
名校通行證有效作業系列答案科目：高中數學 來源： 題型：
【題目】如圖，BC=2，原點O是BC的中點，點A的坐標為 （ 
，0），點D在平面yOz上，且∠BDC=90°，∠DCB=30°． 
（1）求向量 
的坐標
（2）求向量 
的夾角的余弦值大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知{an}是各項都為正數的等比數列，其前n項和為Sn ， 且S2=3，S4=15．
（1）求數列{an}的通項公式；
（2）若數列{bn}是等差數列，且b3=a3 ， b5=a5 ， 試求數列{bn}的前n項和Mn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地4個蔬菜大棚頂部，陽光照在一棵棵茁壯生長的蔬菜上．這些采用水培、無土栽培方式種植的各類蔬菜，成為該地區居民爭相購買的對象．過去50周的資料顯示，該地周光照量
（小時）都在30以上．其中不足50的周數大約有5周，不低于50且不超過70的周數大約有35周，超過70的大約有10周．根據統計某種改良黃瓜每個蔬菜大棚增加量
（百斤）與每個蔬菜大棚使用農夫1號液體肥料
（千克）之間對應數據為如圖所示的折線圖：
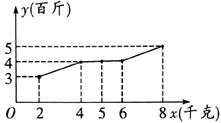
（Ⅰ）依據數據的折線圖，用最小二乘法求出
關于
的線性回歸方程
；并根據所求線性回歸方程，估計如果每個蔬菜大棚使用農夫1號肥料10千克，則這種改良黃瓜每個蔬菜大棚增加量
是多少斤？
（Ⅱ）因蔬菜大棚對光照要求較大，某光照控制儀商家為應對惡劣天氣對光照的影響，為該基地提供了部分光照控制儀，該商家希望安裝的光照控制儀盡可能運行，但每周光照控制儀最多可運行臺數受周光照量
限制，并有如下關系：
周光照量 |
|
|
|
光照控制儀最多可運行臺數 | 3 | 2 | 1 |
若某臺光照控制儀運行，則該臺光照控制儀周利潤為5000元；若某臺光照控制儀未運行，則該臺光照控制儀周虧損800元，欲使商家周總利潤的均值達到最大，應安裝光照控制儀多少臺？
附：回歸方程系數公式：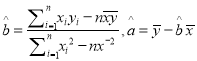 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于定義域為D的函數y=f（x），若同時滿足下列條件：
①f（x）在D內單調遞增或單調遞減；
②存在區間[a，b]D，使f（x）在[a，b]上的值域為[a，b]，則把y=f（x），x∈D叫閉函數．
（1）求閉函數y=x3符合條件②的區間[a，b]；
（2）判斷函數f（x）= 
x+ 
，（x＞0）是否為閉函數？并說明理由；
（3）已知[a，b]是正整數，且定義在（1，m）的函數y=k﹣ 
是閉函數，求正整數m的最小值，及此時實數k的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
