
【題目】設(shè)數(shù)列{an}的前n項(xiàng)和為Sn . 已知a1=1, ![]() =an+1﹣
=an+1﹣ ![]() n2﹣n﹣
n2﹣n﹣ ![]() ,n∈N* .
,n∈N* .
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)設(shè)數(shù)列{bn}滿足an﹣an﹣1=bna ![]() ,求數(shù)列{bn}的n前項(xiàng)和Tn;
,求數(shù)列{bn}的n前項(xiàng)和Tn;
(3)是否存在實(shí)數(shù)λ,使得不等式λa ![]() ﹣
﹣ ![]() +a
+a ![]() +
+ ![]() ≥0恒成立,若存在,求出λ的取值范圍;若不存在,請(qǐng)說(shuō)明理由.
≥0恒成立,若存在,求出λ的取值范圍;若不存在,請(qǐng)說(shuō)明理由.
【答案】
(1)解:∵ ![]() ,n∈N*.
,n∈N*.
∴ ![]() ①
①
∴當(dāng)n≥2時(shí), ![]() ②
②
由①﹣②,得
2Sn﹣2Sn﹣1=nan+1﹣(n﹣1)an﹣n(n+1).
∵2an=2Sn﹣2Sn﹣1
∴2an=nan+1﹣(n﹣1)an﹣n(n+1),
∴ ![]() ,
,
∴數(shù)列 ![]() 是以首項(xiàng)為
是以首項(xiàng)為 ![]() ,公差為1的等差數(shù)列.
,公差為1的等差數(shù)列.
∴ ![]() ,
,
∴ ![]() ,當(dāng)n=1時(shí),上式顯然成立.
,當(dāng)n=1時(shí),上式顯然成立.
∴ ![]()
(2)an﹣an﹣1=bna ![]() bn=
bn= ![]() =
= ![]() =
= ![]() .
.
∴Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .①
.①
![]() Tn=
Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .②
.②
由①﹣②,得
![]() Tn=
Tn= ![]() +2(
+2( ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() )﹣
)﹣ ![]() .
.
= ![]() +2
+2 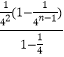 ﹣
﹣ ![]() .
.
∴Tn= ![]() ﹣
﹣ ![]() ,n∈N+
,n∈N+
(3)λa ![]() ﹣
﹣ ![]() +a
+a ![]() +
+ ![]() ≥0λ(2n﹣
≥0λ(2n﹣ ![]() )+2n+
)+2n+ ![]() ≥0,(n=2,4,6,8,10…)λ(2n﹣
≥0,(n=2,4,6,8,10…)λ(2n﹣ ![]() )+(2n﹣
)+(2n﹣ ![]() )2+2≥0,
)2+2≥0,
令t=2n﹣ ![]() ,則t≥
,則t≥ ![]() ,
,
原不等式λt+t2+2≤0≥﹣(t+ ![]() ).
).
∵t+ ![]() 在(
在( ![]() ,+∞)上單調(diào)遞增,
,+∞)上單調(diào)遞增,
∴t+ ![]() ≥
≥ ![]() +
+ ![]() .
.
∴λ≥﹣ ![]()
【解析】(1)需要分類討論:n=1和n≥2兩種情況下的通項(xiàng)公式.當(dāng)n≥2時(shí),根據(jù)已知條件可以推知2Sn﹣2Sn﹣1=nan+1﹣(n﹣1)an﹣n(n+1).2an=nan+1﹣(n﹣1)an﹣n(n+1),由著兩個(gè)式子可以得到數(shù)列 ![]() 是以首項(xiàng)為
是以首項(xiàng)為 ![]() ,公差為1的等差數(shù)列.由此寫出通項(xiàng)公式即可;(2)由an﹣an﹣1=bna
,公差為1的等差數(shù)列.由此寫出通項(xiàng)公式即可;(2)由an﹣an﹣1=bna ![]() 可得bn=
可得bn= ![]() =
= ![]() =
= ![]() .再利用“錯(cuò)位相減法”與等比數(shù)列的求和公式即可得出;(3)將已知不等式變形為λ(2n﹣
.再利用“錯(cuò)位相減法”與等比數(shù)列的求和公式即可得出;(3)將已知不等式變形為λ(2n﹣ ![]() )+(2n﹣
)+(2n﹣ ![]() )2+2≥0,然后結(jié)合函數(shù)的單調(diào)性來(lái)求λ的取值范圍.
)2+2≥0,然后結(jié)合函數(shù)的單調(diào)性來(lái)求λ的取值范圍.
【考點(diǎn)精析】解答此題的關(guān)鍵在于理解數(shù)列的前n項(xiàng)和的相關(guān)知識(shí),掌握數(shù)列{an}的前n項(xiàng)和sn與通項(xiàng)an的關(guān)系 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是正方形,側(cè)棱PD⊥底面ABCD,PD=DC,E是PC的中點(diǎn),作EF⊥PB交PB于點(diǎn)F. 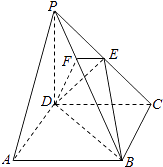
(1)證明PA∥平面EDB;
(2)證明PB⊥平面EFD;
(3)求二面角C﹣PB﹣D的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線C:y2=2px過(guò)點(diǎn)P(1,1).過(guò)點(diǎn)(0,![]() )作直線l與拋物線C交于不同的兩點(diǎn)M,N,過(guò)點(diǎn)M作x軸的垂線分別與直線OP、ON交于點(diǎn)A,B,其中O為原點(diǎn).
)作直線l與拋物線C交于不同的兩點(diǎn)M,N,過(guò)點(diǎn)M作x軸的垂線分別與直線OP、ON交于點(diǎn)A,B,其中O為原點(diǎn).
(Ⅰ)求拋物線C的方程,并求其焦點(diǎn)坐標(biāo)和準(zhǔn)線方程;
(Ⅱ)求證:A為線段BM的中點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在“一帶一路”的建設(shè)中,中石化集團(tuán)獲得了某地深海油田區(qū)塊的開(kāi)采權(quán),集團(tuán)在該地區(qū)隨機(jī)初步勘探了幾口井,取得了地質(zhì)資料.進(jìn)入全面勘探時(shí)期后,集團(tuán)按網(wǎng)絡(luò)點(diǎn)來(lái)布置井位進(jìn)行全面勘探.由于勘探一口井的費(fèi)用很高,如果新設(shè)計(jì)的井位與原有井位重合或接近,便利用舊井的地質(zhì)資料,不必打這口新井,以節(jié)約勘探費(fèi)用.勘探初期數(shù)據(jù)資料下表:
井號(hào)I | 1 | 2 | 3 | 4 | 5 | 6 |
坐標(biāo) |
|
|
|
|
|
|
鉆探深度 | 2 | 4 | 5 | 6 | 8 | 10 |
出油量 | 40 | 70 | 110 | 90 | 160 | 205 |
(1)在散點(diǎn)圖中![]() 號(hào)舊井位置大致分布在一條直線附近,借助前5組數(shù)據(jù)求得回歸線方程為
號(hào)舊井位置大致分布在一條直線附近,借助前5組數(shù)據(jù)求得回歸線方程為![]() ,求
,求![]() ,并估計(jì)
,并估計(jì)![]() 的預(yù)報(bào)值;
的預(yù)報(bào)值;
(2)現(xiàn)準(zhǔn)備勘探新井![]() ,若通過(guò)1、3、5、7號(hào)井計(jì)算出的
,若通過(guò)1、3、5、7號(hào)井計(jì)算出的![]() 的值(
的值(![]() 精確到0.01)相比于(1)中
精確到0.01)相比于(1)中![]() 的值之差(即:
的值之差(即: ![]() )不超過(guò)10%,則使用位置最接近的已有舊井
)不超過(guò)10%,則使用位置最接近的已有舊井![]() ,否則在新位置打井,請(qǐng)判斷可否使用舊井?(參考公式和計(jì)算結(jié)果:
,否則在新位置打井,請(qǐng)判斷可否使用舊井?(參考公式和計(jì)算結(jié)果: 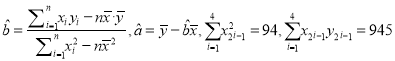 )
)
(3)設(shè)出油量與鉆探深度的比值![]() 不低于20的勘探井稱為優(yōu)質(zhì)井,在原有井號(hào)
不低于20的勘探井稱為優(yōu)質(zhì)井,在原有井號(hào)![]() 的井中任意勘探3口井,求恰好2口是優(yōu)質(zhì)井的概率.
的井中任意勘探3口井,求恰好2口是優(yōu)質(zhì)井的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在△ABC中,內(nèi)角A、B、C的對(duì)邊分別為a,b,c,且a>c,已知 ![]()
![]() =2,cosB=
=2,cosB= ![]() ,b=3,求:
,b=3,求:
(Ⅰ)a和c的值;
(Ⅱ)cos(B﹣C)的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,橢圓
,橢圓![]() 過(guò)點(diǎn)
過(guò)點(diǎn) ,直線
,直線![]() 交
交![]() 軸于
軸于![]() ,且
,且![]() ,
, ![]() 為坐標(biāo)原點(diǎn).
為坐標(biāo)原點(diǎn).
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() 是橢圓
是橢圓![]() 的上頂點(diǎn),過(guò)點(diǎn)
的上頂點(diǎn),過(guò)點(diǎn)![]() 分別作直線
分別作直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點(diǎn),設(shè)這兩條直線的斜率分別為
兩點(diǎn),設(shè)這兩條直線的斜率分別為![]() ,且
,且![]() ,證明:直線
,證明:直線![]() 過(guò)定點(diǎn).
過(guò)定點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)為定義在R上的奇函數(shù),且當(dāng)x>0時(shí),f(x)=log3x,
(1)求f(x)的解析式;
(2)解不等式f(x)≤2.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知向量 ![]() ,
, ![]() 滿足|
滿足| ![]() |=
|= ![]() ,|
,| ![]() |=1,且對(duì)任意實(shí)數(shù)x,不等式|
|=1,且對(duì)任意實(shí)數(shù)x,不等式| ![]() +x
+x ![]() |≥|
|≥| ![]() +
+ ![]() |恒成立,設(shè)
|恒成立,設(shè) ![]() 與
與 ![]() 的夾角為θ,則tan2θ=( )
的夾角為θ,則tan2θ=( )
A.﹣ ![]()
B.![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)f(x)=(1-x2)ex.
(1)討論f(x)的單調(diào)性;
(2)當(dāng)x![]() 0時(shí),f(x)
0時(shí),f(x)![]() ax+1,求a的取值范圍.
ax+1,求a的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com