
【題目】設![]() 外接圓上三段弧
外接圓上三段弧![]() 的中點依次為
的中點依次為![]() ,其關于
,其關于![]() 的對稱點依次為
的對稱點依次為![]() .若頂點與對應旁切圓切點的連線交于一點
.若頂點與對應旁切圓切點的連線交于一點![]() (界心),
(界心),![]() 為
為![]() 的垂心,證明:
的垂心,證明:![]() 在以
在以![]() 為直徑的圓上.
為直徑的圓上.
【答案】見解析
【解析】
記![]() 的三邊長為
的三邊長為![]() ,
,![]() ,
,![]() 為
為![]() 的內心.
的內心.
先證明一個引理.
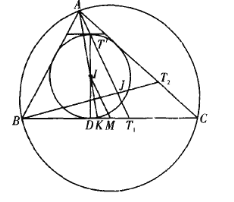
引理 頂點與界心連線平行且等于2倍內心與其對應邊中點的連線.
證明:如圖,設![]() 為
為![]() 的內心,
的內心,![]() 為
為![]() 的中點,
的中點,![]() 為切點,
為切點,![]() 為對應角平分線的交點,
為對應角平分線的交點,![]() 為旁切圓的切點,
為旁切圓的切點,![]() 為界心,
為界心,![]() 為
為![]() 與內切圓的交點.
與內切圓的交點.
對![]() 與截線
與截線![]() 應用梅涅勞斯定理得
應用梅涅勞斯定理得![]() .
.
將![]() ,
,![]() ,
,![]() ,代入上式化簡得
,代入上式化簡得![]()
因為![]() 為
為![]() 的中點,
的中點,![]() 為切點,
為切點,![]() 為旁切圓的切點,所以,
為旁切圓的切點,所以,![]() .
.
由位似變換,知![]() 為
為![]() 的中點.
的中點.
故![]() .
.
回到原題.如圖,延長![]() 與
與![]() 的延長線交于點
的延長線交于點![]() .
.
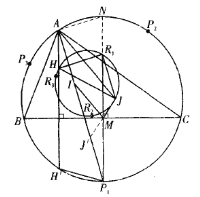
由引理,知![]() ,且
,且![]() 所以,
所以,![]() 為
為![]() 的中點.
的中點.
又點![]() 與
與![]() 關于
關于![]() 對稱,于是.由對角線互柑平分的性質,知四邊形
對稱,于是.由對角線互柑平分的性質,知四邊形![]() 為平行四邊形.
為平行四邊形.
因此, ![]() .
.
延長![]() 與外接圓交于點
與外接圓交于點![]() ,聯結
,聯結![]() .
.
因為![]() 為垂心,
為垂心,![]() 關于
關于![]() 的對稱點
的對稱點![]() 在外接圓上,所以,
在外接圓上,所以,![]() .
.
于是,![]() .則
.則![]() .
.
從而,四邊形![]() 為平行四邊形.
為平行四邊形.
又![]() 為外接圓的直徑,故
為外接圓的直徑,故![]() .易知,
.易知, ![]() .
.
所以, ![]() ,
,
同理, ![]() ,
,![]() .故本題得證.
.故本題得證.


科目:高中數學 來源: 題型:
【題目】某中學將要舉行校園歌手大賽,現有4男3女參加,需要安排他們的出場順序.(結果用數字作答)
(1)如果3個女生都不相鄰,那么有多少種不同的出場順序?
(2)如果3位女生都相鄰,且男生甲不在第一個出場,那么有多少種不同的出場順序?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018以來,依托用戶碎片化時間的娛樂需求、分享需求以及視頻態的信息負載力,短視頻快速崛起;與此同時,移動閱讀方興未艾,從側面反應了人們對精神富足的一種追求,在習慣了大眾娛樂所帶來的短暫愉悅后,部分用戶依舊對有著傳統文學底蘊的嚴肅閱讀青睞有加.某讀書APP抽樣調查了非一線城市![]() 和一線城市
和一線城市![]() 各100名用戶的日使用時長(單位:分鐘),繪制成頻率分布直方圖如下,其中日使用時長不低于60分鐘的用戶記為“活躍用戶”.
各100名用戶的日使用時長(單位:分鐘),繪制成頻率分布直方圖如下,其中日使用時長不低于60分鐘的用戶記為“活躍用戶”.
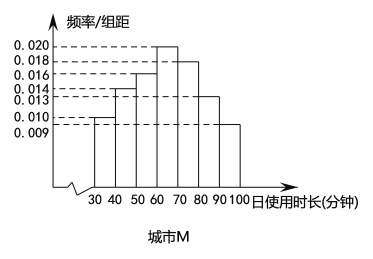
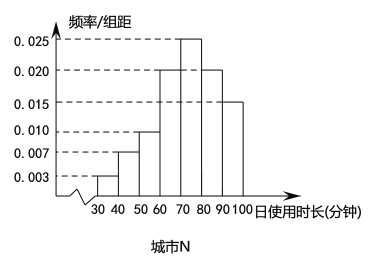
(1)請填寫以下![]() 列聯表,并判斷是否有99%的把握認為用戶活躍與否與所在城市有關?
列聯表,并判斷是否有99%的把握認為用戶活躍與否與所在城市有關?
活躍用戶 | 不活躍用戶 | 合計 | |
城市 | |||
城市 | |||
合計 |
臨界值表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
參考公式: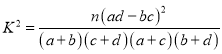 .
.
(2)以頻率估計概率,從城市![]() 中任選2名用戶,從城市
中任選2名用戶,從城市![]() 中任選1名用戶,設這3名用戶中活躍用戶的人數為
中任選1名用戶,設這3名用戶中活躍用戶的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
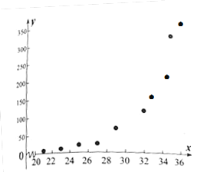
【題目】經觀測,某昆蟲的產卵數![]() 與溫度
與溫度![]() 有關,現將收集到的溫度
有關,現將收集到的溫度![]() 和產卵數
和產卵數![]() 的10組觀測數據作了初步處理,得到如圖的散點圖及一些統計量表.
的10組觀測數據作了初步處理,得到如圖的散點圖及一些統計量表.
|
|
|
|
|
|
275 | 731.1 | 21.7 | 150 | 2368.36 | 30 |
表中![]() ,
,![]()
(1)根據散點圖判斷,![]() ,
,![]() 與
與![]() 哪一個適宜作為
哪一個適宜作為![]() 與
與![]() 之間的回歸方程模型?(給出判斷即可,不必說明理由)
之間的回歸方程模型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果及表中數據.
①試求![]() 關于
關于![]() 回歸方程;
回歸方程;
②已知用人工培養該昆蟲的成本![]() 與溫度
與溫度![]() 和產卵數
和產卵數![]() 的關系為
的關系為![]() ,當溫度
,當溫度![]() (
(![]() 取整數)為何值時,培養成本的預報值最小?
取整數)為何值時,培養成本的預報值最小?
附:對于一組數據![]() ,
,![]() ,
,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為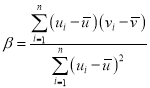 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,定點
,定點![]() ,定直線
,定直線![]() 和
和![]() 上的動點
上的動點![]() 滿足:
滿足:![]() 在直線
在直線![]() 的同側,點
的同側,點![]() 在直線
在直線![]() 的另一側.以
的另一側.以![]() 為焦點作與直線
為焦點作與直線![]() 相切的橢圓
相切的橢圓![]() ,且當
,且當![]() 在
在![]() 上運動時,橢圓
上運動時,橢圓![]() 的長軸長為定值.
的長軸長為定值.
(1)求直線![]() 的方程;
的方程;
(2)對于第一象限內任意2012個在橢圓![]() 上的點,是否一定可以將它們分成兩組,使得其中一組點的橫坐標之和不大于2013,另一組點的縱坐標之和不大于2013?請證明你的結論.
上的點,是否一定可以將它們分成兩組,使得其中一組點的橫坐標之和不大于2013,另一組點的縱坐標之和不大于2013?請證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于數列![]() ,若存在正數p,使得
,若存在正數p,使得![]() 對任意
對任意![]() 都成立,則稱數列
都成立,則稱數列![]() 為“擬等比數列”.
為“擬等比數列”.
![]() 已知
已知![]() ,
,![]() 且
且![]() ,若數列
,若數列![]() 和
和![]() 滿足:
滿足:![]() ,
,![]() 且
且![]() ,
,![]() .
.
![]() 若
若![]() ,求
,求![]() 的取值范圍;
的取值范圍;
![]() 求證:數列
求證:數列![]() 是“擬等比數列”;
是“擬等比數列”;
![]() 已知等差數列
已知等差數列![]() 的首項為
的首項為![]() ,公差為d,前n項和為
,公差為d,前n項和為![]() ,若
,若![]() ,
,![]() ,
,![]() ,且
,且![]() 是“擬等比數列”,求p的取值范圍
是“擬等比數列”,求p的取值范圍![]() 請用
請用![]() ,d表示
,d表示![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】11個興趣班,若干學生參與(可重復參與),每個興趣班人數相同(招滿,人數未知).已知任意九個興趣班包括了全體學生,而任意八個興趣班沒有包括全體學生求學生總人數的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com