
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,左、右焦點分別是
,左、右焦點分別是![]() ,橢圓
,橢圓![]() 上短軸的一個端點與兩個焦點構成的三角形的面積為
上短軸的一個端點與兩個焦點構成的三角形的面積為![]() ;
;
(1)求橢圓![]() 的方程;
的方程;
(2)過![]() 作垂直于
作垂直于![]() 軸的直線
軸的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點(點
兩點(點![]() 在第二象限),
在第二象限),![]() 是橢圓上位于直線
是橢圓上位于直線![]() 兩側的動點,若
兩側的動點,若![]() ,求證:直線
,求證:直線![]() 的斜率為定值.
的斜率為定值.
 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源: 題型:
【題目】2019年是中國成立70周年,也是全面建成小康社會的關鍵之年.為了迎祖國70周年生日,全民齊心奮力建設小康社會,某校特舉辦“喜迎國慶,共建小康”知識競賽活動.下面的莖葉圖是參賽兩組選手答題得分情況,則下列說法正確的是( )
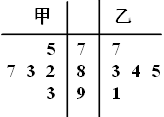
A.甲組選手得分的平均數(shù)小于乙組選手的平均數(shù)B.甲組選手得分的中位數(shù)大于乙組選手的中位數(shù)
C.甲組選手得分的中位數(shù)等于乙組選手的中位數(shù)D.甲組選手得分的方差大于乙組選手的的方差
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調區(qū)間;
的單調區(qū)間;
(2)當![]() 時,證明:
時,證明: ![]() (其中e為自然對數(shù)的底數(shù)).
(其中e為自然對數(shù)的底數(shù)).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,PA⊥AB,PA=1,PC=3,BC=2,sin∠PCA![]() ,E,F,G分別為線段的PC,PB,AB中點,且BE
,E,F,G分別為線段的PC,PB,AB中點,且BE![]() .
.
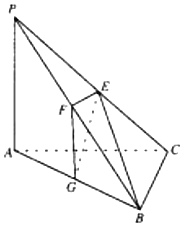
(1)求證:AB⊥BC;
(2)若M為線段BC上一點,求三棱錐M﹣EFG的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() 是
是![]() 的一個極值點
的一個極值點
(1)求實數(shù)![]() 的值,并證明:當
的值,并證明:當![]() 時,
時,![]() 恒成立;
恒成立;
(2)若函數(shù)![]() ,試討論函數(shù)
,試討論函數(shù)![]() 的零點個數(shù)
的零點個數(shù)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() ,
, ![]() 滿足約束條件
滿足約束條件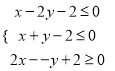 ,若
,若![]() 取得最大值的最優(yōu)解不唯一,則實數(shù)
取得最大值的最優(yōu)解不唯一,則實數(shù)![]() 的值為__________.
的值為__________.
【答案】![]() 或
或![]()
【解析】由題可知若![]() 取得最大值的最優(yōu)解不唯一則
取得最大值的最優(yōu)解不唯一則![]() 必平行于可行域的某一邊界,如圖:
必平行于可行域的某一邊界,如圖: 要Z最大則直線與y軸的截距最大即可,當a<0時,則平行AC直線即可故a=-2,當a>0時,則直線平行AB即可,故a=1
要Z最大則直線與y軸的截距最大即可,當a<0時,則平行AC直線即可故a=-2,當a>0時,則直線平行AB即可,故a=1
點睛:線性規(guī)劃為常考題型,解決此題務必要理解最優(yōu)解個數(shù)為無數(shù)個時的條件是什么,然后根據(jù)幾何關系求解即可
【題型】填空題
【結束】
16
【題目】《數(shù)書九章》三斜求積術:“以小斜冪,并大斜冪,減中斜冪,余半之,自乘于上;以小斜冪乘大斜冪,減上,余四約一,為實,一為從隅,開平方得積”.秦九韶把三角形的三條邊分別稱為小斜、中斜和大斜,“術”即方法.以![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別表示三角形的面積,大斜,中斜,小斜;
分別表示三角形的面積,大斜,中斜,小斜; ![]() ,
, ![]() ,
, ![]() 分別為對應的大斜,中斜,小斜上的高;則
分別為對應的大斜,中斜,小斜上的高;則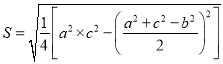
![]()
![]() .若在
.若在![]() 中
中![]() ,
, ![]() ,
, ![]() ,根據(jù)上述公式,可以推出該三角形外接圓的半徑為__________.
,根據(jù)上述公式,可以推出該三角形外接圓的半徑為__________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】給出以下四個結論:
(1)函數(shù)![]() 的對稱中心是
的對稱中心是![]() ;
;
(2)若關于![]() 的方程
的方程![]() 在
在![]() 沒有實數(shù)根,則
沒有實數(shù)根,則![]() 的取值范圍是
的取值范圍是![]() ;
;
(3)已知點![]() 與點
與點![]() 在直線
在直線![]() 兩側,則
兩側,則![]() ;
;
(4)若將函數(shù)![]() 的圖象向右平移
的圖象向右平移![]() 個單位后變?yōu)榕己瘮?shù),則
個單位后變?yōu)榕己瘮?shù),則![]() 的最小值是
的最小值是![]() ;
;
其中正確的結論是:_____________________(把所有正確命題的序號填上).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
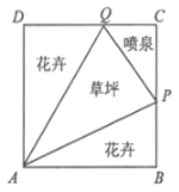
【題目】如圖所示,我市某居民小區(qū)擬在邊長為1百米的正方形地塊![]() 上劃出一個三角形地塊
上劃出一個三角形地塊![]() 種植草坪,兩個三角形地塊
種植草坪,兩個三角形地塊![]() 與
與![]() 種植花卉,一個三角形地塊
種植花卉,一個三角形地塊![]() 設計成水景噴泉,四周鋪設小路供居民平時休閑散步,點
設計成水景噴泉,四周鋪設小路供居民平時休閑散步,點![]() 在邊
在邊![]() 上,點
上,點![]() 在邊
在邊![]() 上,記
上,記![]() .
.
(1)當![]() 時,求花卉種植面積
時,求花卉種植面積![]() 關于
關于![]() 的函數(shù)表達式,并求
的函數(shù)表達式,并求![]() 的最小值;
的最小值;
(2)考慮到小區(qū)道路的整體規(guī)劃,要求![]() ,請?zhí)骄?/span>
,請?zhí)骄?/span>![]() 是否為定值,若是,求出此定值,若不是,請說明理由.
是否為定值,若是,求出此定值,若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C的參數(shù)為![]() (α為參數(shù)),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為
(α為參數(shù)),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為![]() ;
;
(1)寫出曲線C的普通方程和直線l的參數(shù)方程;
(2)設點P(m,0),若直線l與曲線C相交于A,B兩點,且|PA|![]() |PB|=1,求實數(shù)m的值.
|PB|=1,求實數(shù)m的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com