【題目】《九章算術》是我國古代內容極為豐富的數學名著，書中有一個“引葭赴岸”問題：“今有池方一丈，葭生其中央.出水一尺，引葭赴岸，適與岸齊.問水深、葭長各幾何？”其意思為“今有水池1丈見方（即
尺），蘆葦生長在水的中央，長出水面的部分為1尺.將蘆葦向池岸牽引，恰巧與水岸齊接（如圖所示）.試問水深、蘆葦的長度各是多少？假設
，現有下述四個結論：
①水深為12尺；②蘆葦長為15尺；③
；④
.
其中所有正確結論的編號是（ ）
A.①③B.①③④C.①④D.②③④
科目：高中數學 來源： 題型：
【題目】設橢圓
的左右焦點分別為F1，F2，點P 在橢圓上運動， 
的最大值為m， 
的最小值為n，且m≥2n，則該橢圓的離心率的取值范圍為________
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分13分）已知函數
（
為常數，
）
（1）若
是函數
的一個極值點，求
的值；
（2）求證：當
時，
在
上是增函數；
（3）若對任意的
，總存在
，使不等式
成立，求正實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
的頂點為坐標原點，焦點
在
軸的正半軸上，過焦點
作斜率為
的直線交拋物線
于
兩點，且
，其中
為坐標原點.
（1）求拋物線
的方程；
（2）設點
，直線
分別交準線
于點
，問：在
軸的正半軸上是否存在定點
，使
，若存在，求出定點
的坐標，若不存在，試說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某家庭進行理財投資，根據長期收益率市場預測，投資債券等穩健型產品的年收益與投資額成正比，投資股票等風險型產品的年收益與投資額的算術平方根成正比．已知投資1萬元時兩類產品的年收益分別為0.125萬元和0.5萬元（如圖）．
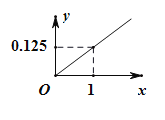
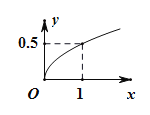
（1）分別寫出兩種產品的年收益與投資額的函數關系式；
（2）該家庭現有20萬元資金，全部用于理財投資，問：怎么分配資金能使投資獲得最大年收益，其最大年收益是多少萬元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，
為平行四邊形ABCD所在平面外一點，M,N分別為AB,PC的中點，平面PAD
平面PBC＝
.
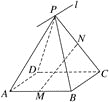
(1)求證：BC∥；
(2)MN與平面PAD是否平行？試證明你的結論．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
