
【題目】在發生某公共衛生事件期間,有專業機構認為該事件在一段時間內沒有發生大規模群體感染的標志是“連續10天,每天新增疑似病例不超過7人”.根據過去10天甲、乙、丙、丁四地新增疑似病例數據,一定符合該標志的是( )
A.甲地:總體均值為3,中位數為4B.乙地:中位數為2,眾數為3
C.丙地:總體均值為2,總體方差為3D.丁地:總體均值為1,總體方差大于0
科目:高中數學 來源: 題型:
【題目】對某兩名高三學生在連續9次數學測試中的成績(單位:分)進行統計得到如下折線圖。下面關于這兩位同學的數學成績的分析中,正確的共有( )個。

①甲同學的成績折線圖具有較好的對稱性,與正態曲線相近,故而平均成績為130分;
②根據甲同學成績折線圖提供的數據進行統計,估計該同學平均成績在區間![]() 內;
內;
③乙同學的數學成績與考試次號具有比較明顯的線性相關性,且為正相關;
④乙同學在這連續九次測驗中的最高分與最低分的差超過40分。
A.1 B.2
C.3 D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有一張長為80cm、寬為60cm的長方形鐵皮ABCD,準備用它做成一只無蓋長方體鐵皮盒,要求材料利用率為100%,不考慮焊接處損失.如圖,若長方形ABCD的一個角剪下一塊正方形鐵皮,作為鐵皮盒的底面,用余下材料剪拼后作為鐵皮盒的側面,設長方體的底面正方形邊長為x(cm),高為y(cm),體積為V(cm3).求:
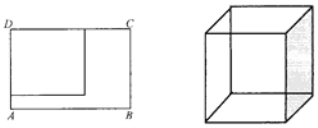
(1)y關于x的表達式;
(2)該鐵皮盒體積V的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解本市的交通狀況,某校高一年級的同學分成了甲、乙、丙三個組,從下午13點到18點,分別對三個路口的機動車通行情況進行了實際調查,并繪制了頻率分布直方圖(如圖),記甲、乙、丙三個組所調查數據的標準差分別為![]() ,則它們的大小關系為( )
,則它們的大小關系為( )



A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分13分)設數列![]() 的前
的前![]() 項和為
項和為![]() .已知
.已知![]() ,
, ![]() ,
, ![]() .
.
(1)寫出![]() 的值,并求數列
的值,并求數列![]() 的通項公式;
的通項公式;
(2)記![]() 為數列
為數列![]() 的前
的前![]() 項和,求
項和,求![]() ;
;
(3)若數列![]() 滿足
滿足![]() ,
, ![]() ,求數列
,求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班級有50名學生,其中有30名男生和20名女生,隨機詢問了該班5名男生和5名女生在某次數學測驗中的成績,5名男生的成績分別為86,94,88,92,90,5名女生的成績分別為88,93,93,88,93.
①這種抽樣方法是一種分層隨機抽樣;
②這5名男生成績的方差大于這5名女生成績的方差;
③該班男生成績的平均數小于該班女生成績的平均數.
則以上說法一定正確的是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車駕駛學校在學員結業前,對學員的駕駛技術進行4次考核,規定:按順序考核,一旦考核合格就不必參加以后的考核,否則還需參加下次考核。若學員小李獨立參加每次考核合格的概率依次組成一個公差為![]() 的等差數列,他參加第一次考核合格的概率不超過
的等差數列,他參加第一次考核合格的概率不超過![]() ,且他直到參加第二次考核才合格的概率為
,且他直到參加第二次考核才合格的概率為![]() .
.
(1)求小李第一次參加考核就合格的概率![]() ;
;
(2)求小李參加考核的次數![]() 的分布列和數學期望
的分布列和數學期望
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)![]() 為曲線
為曲線![]() 上的動點,點
上的動點,點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() ,求點
,求點![]() 的軌跡
的軌跡![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的極坐標為
的極坐標為![]() ,點
,點![]() 在曲線
在曲線![]() 上,求
上,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com