
【題目】已知函數![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)若![]() 存在兩個極值點
存在兩個極值點![]() ,證明:
,證明:![]() .
.
【答案】(1)當![]() 時,
時,![]() 在
在![]() 單調遞減.,
單調遞減.,
當![]() 時,
時, ![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增.
單調遞增.
(2)證明見解析.
【解析】分析:(1)首先確定函數的定義域,之后對函數求導,之后對![]() 進行分類討論,從而確定出導數在相應區間上的符號,從而求得函數對應的單調區間;
進行分類討論,從而確定出導數在相應區間上的符號,從而求得函數對應的單調區間;
(2)根據![]() 存在兩個極值點,結合第一問的結論,可以確定
存在兩個極值點,結合第一問的結論,可以確定![]() ,令
,令![]() ,得到兩個極值點
,得到兩個極值點![]() 是方程
是方程![]() 的兩個不等的正實根,利用韋達定理將其轉換,構造新函數證得結果.
的兩個不等的正實根,利用韋達定理將其轉換,構造新函數證得結果.
詳解:(1)![]() 的定義域為
的定義域為![]() ,
,![]() .
.
(i)若![]() ,則
,則![]() ,當且僅當
,當且僅當![]() ,
,![]() 時
時![]() ,所以
,所以![]() 在
在![]() 單調遞減.
單調遞減.
(ii)若![]() ,令
,令![]() 得,
得,![]() 或
或![]() .
.
當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() .所以
.所以![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增.
單調遞增.
(2)由(1)知,![]() 存在兩個極值點當且僅當
存在兩個極值點當且僅當![]() .
.
由于![]() 的兩個極值點
的兩個極值點![]() 滿足
滿足![]() ,所以
,所以![]() ,不妨設
,不妨設![]() ,則
,則![]() .由于
.由于
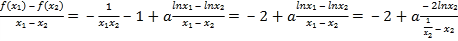 ,
,
所以![]() 等價于
等價于![]() .
.
設函數![]() ,由(1)知,
,由(1)知,![]() 在
在![]() 單調遞減,又
單調遞減,又![]() ,從而當
,從而當![]() 時,
時,![]() .
.
所以![]() ,即
,即![]() .
.


科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代的數學名著,書中把三角形的田稱為“圭田”,把直角梯形的田稱為“邪田”,稱底是“廣”,稱高是“正從”,“步”是丈量土地的單位.現有一邪田,廣分別為十步和二十步,正從為十步,其內有一塊廣為八步,正從為五步的圭田.若在邪田內隨機種植一株茶樹,求該株茶樹恰好種在圭田內的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區2008年至2016年糧食產量的部分數據如下表:

(1)求該地區2008年至2016年的糧食年產量![]() 與年份
與年份![]() 之間的線性回歸方程;
之間的線性回歸方程;
(2)利用(1)中的回歸方程,分析2008年至2016年該地區糧食產量的變化情況,并預測該地區 2018年的糧食產量.
附:回歸直線的斜率和截距的最小二乘估計公式分別為 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有![]() 個小球,甲、乙兩位同學輪流且不放回抓球,每次最少抓1個球,最多抓3個球,規定誰抓到最后一個球贏.如果甲先抓,那么下列推斷正確的是_____________.(填寫序號)
個小球,甲、乙兩位同學輪流且不放回抓球,每次最少抓1個球,最多抓3個球,規定誰抓到最后一個球贏.如果甲先抓,那么下列推斷正確的是_____________.(填寫序號)
①若![]() ,則甲有必贏的策略; ②若
,則甲有必贏的策略; ②若![]() ,則乙有必贏的策略;
,則乙有必贏的策略;
③若![]() ,則甲有必贏的策略; ④若
,則甲有必贏的策略; ④若![]() ,則乙有必贏的策略.
,則乙有必贏的策略.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com