
【題目】已知橢圓![]() 的離心率
的離心率![]() ,且橢圓
,且橢圓![]() 與圓
與圓![]() 的4個交點恰為一個正方形的4個頂點.
的4個交點恰為一個正方形的4個頂點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知點![]() 為橢圓
為橢圓![]() 的下頂點,
的下頂點, ![]() 為橢圓
為橢圓![]() 上與
上與![]() 不重合的兩點,若直線
不重合的兩點,若直線![]() 與直線
與直線![]() 的斜率之和為
的斜率之和為![]() ,試判斷是否存在定點
,試判斷是否存在定點![]() ,使得直線
,使得直線![]() 恒過點
恒過點![]() ,若存在,求出點
,若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1) ![]() (2) 存在定點
(2) 存在定點![]() ,使得直線
,使得直線![]() 恒過點
恒過點![]()
【解析】試題分析:(1)第(1)問,直接根據已知條件得到關于a,b的一個方程組,再解方程組即可. (2)第(2)問,對直線![]() 的斜率分兩種情況討論.每一種情況都要先根據已知條件求直線DE的方程,再判斷其方程是否過定點.
的斜率分兩種情況討論.每一種情況都要先根據已知條件求直線DE的方程,再判斷其方程是否過定點.
試題解析:
(1)因為橢圓![]() 的離心率
的離心率![]() ,
,
所以![]() ,即
,即![]() ,
,
因為橢圓![]() 與圓
與圓![]() 的4個交點恰為一個正方形的4個頂點,
的4個交點恰為一個正方形的4個頂點,
所以直線![]() 與圓
與圓![]() 的一個交點
的一個交點 在橢圓
在橢圓![]() 上,所以
上,所以![]() ,
,
由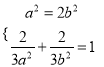 解得
解得![]() ,所以橢圓
,所以橢圓![]() 的標準方程為
的標準方程為![]() .
.
(2)由(1)知![]() ,
,
當直線![]() 的斜率存在時,設直線
的斜率存在時,設直線![]() 的方程為
的方程為![]() ,
,
代入![]() 得,
得, ![]() ,
,
所以![]() ,即
,即![]() .
.
設![]() ,則
,則![]() ,
,
因為直線![]() 與直線
與直線![]() 的斜率之和為
的斜率之和為![]() ,所以
,所以![]()
![]()
![]() ,
,
整理得![]() ,所以直線
,所以直線![]() 的方程為
的方程為![]() ,
,
顯然直線![]() 經過定點
經過定點![]() .
.
當直線![]() 的斜率不存在時,設直線
的斜率不存在時,設直線![]() 的方程為
的方程為![]() ,
,
因為直線![]() 與直線
與直線![]() 的斜率之和為
的斜率之和為![]() ,設
,設![]() ,則
,則![]() ,
,
所以![]() ,解得
,解得![]() ,
,
此時直線![]() 的方程為
的方程為![]() ,顯然直線
,顯然直線![]() 經過定點
經過定點![]() .
.
綜上,存在定點![]() ,使得直線
,使得直線![]() 恒過點
恒過點![]() .
.


科目:高中數學 來源: 題型:
【題目】四棱錐![]() 的底面ABCD是邊長為2的菱形,側面PAD是正三角形,
的底面ABCD是邊長為2的菱形,側面PAD是正三角形,![]() ,E為AD的中點,二面角
,E為AD的中點,二面角![]() 為
為![]() .
.

![]() 證明:
證明:![]() 平面PBE;
平面PBE;
![]() 求點P到平面ABCD的距離;
求點P到平面ABCD的距離;
![]() 求直線BC與平面PAB所成角的正弦值.
求直線BC與平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() :
:![]() ,若存在實數
,若存在實數![]() 使得一條曲線與直線
使得一條曲線與直線![]() 有兩個不同的交點,且以這兩個交點為端點的線段長度恰好等于
有兩個不同的交點,且以這兩個交點為端點的線段長度恰好等于![]() ,則稱此曲線為直線
,則稱此曲線為直線![]() 的“絕對曲線”.下面給出的四條曲線方程:
的“絕對曲線”.下面給出的四條曲線方程:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中直線![]() 的“絕對曲線”的條數為( )
的“絕對曲線”的條數為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:
(單位:![]() )和年利潤
)和年利潤![]() (單位:千元)的影響,對近13年的宣傳費
(單位:千元)的影響,對近13年的宣傳費![]() 和年銷售量
和年銷售量![]()
![]() 數據作了初步處理,得到下面的散點圖及一些統計量的值.
數據作了初步處理,得到下面的散點圖及一些統計量的值.

由散點圖知,按![]() 建立
建立![]() 關于
關于![]() 的回歸方程是合理的.令
的回歸方程是合理的.令![]() ,則
,則![]() ,經計算得如下數據:
,經計算得如下數據:
|
|
|
|
|
|
10.15 | 109.94 | 0.16 | -2.10 | 0.21 | 21.22 |
(1)根據以上信息,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)已知這種產品的年利潤![]() 與
與![]() 的關系為
的關系為![]() .根據(1)的結果,求當年宣傳費
.根據(1)的結果,求當年宣傳費![]() 時,年利潤的預報值是多少?
時,年利潤的預報值是多少?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,O為坐標原點,以O為圓心的圓與直線
中,O為坐標原點,以O為圓心的圓與直線![]() 相切.
相切.
(1)求圓O的方程.
(2)直線![]() 與圓O交于A,B兩點,在圓O上是否存在一點M,使得四邊形
與圓O交于A,B兩點,在圓O上是否存在一點M,使得四邊形![]() 為菱形?若存在,求出此時直線l的斜率;若不存在,說明理由.
為菱形?若存在,求出此時直線l的斜率;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com