
ĪŠŅ}─┐Ī┐ęčų¬╚²└Ōų∙![]() ųąŻ¼
ųąŻ¼![]() Ż¼
Ż¼![]() Ż¼
Ż¼![]() Ż¼
Ż¼![]() Ż«
Ż«

![]() Ū¾ūCŻ║├µ
Ū¾ūCŻ║├µ![]() ├µ
├µ![]() Ż╗
Ż╗
![]() ╚¶
╚¶![]() Ż¼į┌ŠĆČ╬
Ż¼į┌ŠĆČ╬![]() ╔Ž╩Ūʱ┤µį┌ę╗³c
╔Ž╩Ūʱ┤µį┌ę╗³c![]() Ż¼╩╣Č■├µĮŪ
Ż¼╩╣Č■├µĮŪ![]() Ą─ŲĮ├µĮŪĄ─ėÓŽęųĄ×ķ
Ą─ŲĮ├µĮŪĄ─ėÓŽęųĄ×ķ![]() Ż┐╚¶┤µį┌Ż¼┤_Č©³c
Ż┐╚¶┤µį┌Ż¼┤_Č©³c![]() Ą─╬╗ų├Ż╗╚¶▓╗┤µį┌Ż¼šf├„└Ēė╔
Ą─╬╗ų├Ż╗╚¶▓╗┤µį┌Ż¼šf├„└Ēė╔
ĪŠ┤░ĖĪ┐Ż©1Ż®ęŖĮŌ╬÷Ż╗Ż©2Ż®ęŖĮŌ╬÷
ĪŠĮŌ╬÷Ī┐
![]() ė╔
ė╔![]() Ż¼┐╔Ą├╦─▀ģą╬
Ż¼┐╔Ą├╦─▀ģą╬![]() ×ķ┴Ōą╬Ż¼ät
×ķ┴Ōą╬Ż¼ät![]() Ż¼ėų
Ż¼ėų![]() Ż¼└¹ė├ŠĆ├µ┤╣ų▒Ą─┼ąČ©┐╔Ą├
Ż¼└¹ė├ŠĆ├µ┤╣ų▒Ą─┼ąČ©┐╔Ą├![]() ŲĮ├µ
ŲĮ├µ![]() Ż¼Ą├ĄĮ
Ż¼Ą├ĄĮ![]() Ż¼ĮY(ji©”)║Ž
Ż¼ĮY(ji©”)║Ž![]() Ż¼╝┤┐╔ūC├„
Ż¼╝┤┐╔ūC├„![]() ŲĮ├µ
ŲĮ├µ![]() Ż¼Å─Č°┐╔ūC├„├µ
Ż¼Å─Č°┐╔ūC├„├µ![]() ├µ
├µ![]() Ż╗
Ż╗
![]() ęįC×ķū°ś╦įŁ³cŻ¼ĘųäeęįCAŻ¼CB╦∙į┌ų▒ŠĆ×ķxŻ¼y▌SĮ©┴ó┐šķgų▒ĮŪū°ś╦ŽĄŻ¼įOį┌ŠĆČ╬AC╔Ž┤µį┌ę╗³cPŻ¼ØMūŃ
ęįC×ķū°ś╦įŁ³cŻ¼ĘųäeęįCAŻ¼CB╦∙į┌ų▒ŠĆ×ķxŻ¼y▌SĮ©┴ó┐šķgų▒ĮŪū°ś╦ŽĄŻ¼įOį┌ŠĆČ╬AC╔Ž┤µį┌ę╗³cPŻ¼ØMūŃ![]() Ż¼╩╣Ą├Č■├µĮŪ
Ż¼╩╣Ą├Č■├µĮŪ![]() Ą─ėÓŽęųĄ×ķ
Ą─ėÓŽęųĄ×ķ![]() Ż¼└¹ė├Č■├µĮŪ
Ż¼└¹ė├Č■├µĮŪ![]() Ą─ėÓŽęųĄ×ķ
Ą─ėÓŽęųĄ×ķ![]() Ż¼┐╔Ū¾Ą├
Ż¼┐╔Ū¾Ą├![]() Ą─ųĄŻ¼Å─Č°Ą├ĄĮ┤░ĖĪŻ
Ą─ųĄŻ¼Å─Č°Ą├ĄĮ┤░ĖĪŻ
![]() ūC├„Ż║╚ńłDŻ¼
ūC├„Ż║╚ńłDŻ¼![]() Ż¼
Ż¼![]() ╦─▀ģą╬
╦─▀ģą╬![]() ×ķ┴Ōą╬Ż¼
×ķ┴Ōą╬Ż¼
▀BĮė![]() Ż¼ät
Ż¼ät![]() Ż¼ėų
Ż¼ėų![]() Ż¼Ūę
Ż¼Ūę![]() Ż¼
Ż¼
![]() ŲĮ├µ
ŲĮ├µ![]() Ż¼ät
Ż¼ät![]() Ż¼
Ż¼
ėų![]() Ż¼╝┤
Ż¼╝┤![]() Ż¼
Ż¼![]() ŲĮ├µ
ŲĮ├µ![]() Ż¼
Ż¼
Č°![]() ŲĮ├µ
ŲĮ├µ![]() Ż¼
Ż¼![]() ├µ
├µ![]() ├µ
├µ![]() Ż╗
Ż╗
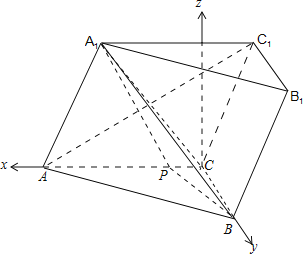
![]() ĮŌŻ║ęįC×ķū°ś╦įŁ³cŻ¼ĘųäeęįCAŻ¼CB╦∙į┌ų▒ŠĆ×ķxŻ¼y▌SĮ©┴ó╚ńłD╦∙╩ŠĄ─┐šķgų▒ĮŪū°ś╦ŽĄŻ¼
ĮŌŻ║ęįC×ķū°ś╦įŁ³cŻ¼ĘųäeęįCAŻ¼CB╦∙į┌ų▒ŠĆ×ķxŻ¼y▌SĮ©┴ó╚ńłD╦∙╩ŠĄ─┐šķgų▒ĮŪū°ś╦ŽĄŻ¼
![]() Ż¼
Ż¼![]() Ż¼
Ż¼![]() Ż¼
Ż¼
![]() 0Ż¼
0Ż¼![]() Ż¼
Ż¼![]() 2Ż¼
2Ż¼![]() Ż¼
Ż¼![]() 0Ż¼
0Ż¼![]() Ż¼
Ż¼![]() 0,
0,![]()
įOį┌ŠĆČ╬![]() ╔Ž┤µį┌ę╗³c
╔Ž┤µį┌ę╗³c![]() Ż¼ØMūŃ
Ż¼ØMūŃ![]() Ż¼╩╣Ą├Č■├µĮŪ
Ż¼╩╣Ą├Č■├µĮŪ![]() Ą─ėÓŽęųĄ×ķ
Ą─ėÓŽęųĄ×ķ![]() Ż«
Ż«
ät![]() Ż«
Ż«
![]() 0Ż¼
0Ż¼![]() Ż¼
Ż¼![]() Ż¼
Ż¼![]() Ż¼
Ż¼![]() Ż¼
Ż¼![]() Ż«
Ż«
įOŲĮ├µ![]() Ą─ę╗éĆĘ©Ž“┴┐×ķ
Ą─ę╗éĆĘ©Ž“┴┐×ķ![]() Ż¼
Ż¼
ė╔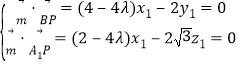 Ż¼╚Ī
Ż¼╚Ī![]() Ż¼Ą├
Ż¼Ą├![]() Ż╗
Ż╗
ŲĮ├µ![]() Ą─ę╗éĆĘ©Ž“┴┐×ķ
Ą─ę╗éĆĘ©Ž“┴┐×ķ![]() Ż«
Ż«
ė╔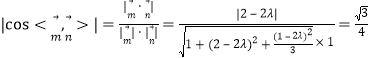 Ż¼
Ż¼
ĮŌĄ├Ż║![]() Ż¼╗“
Ż¼╗“![]() Ż¼
Ż¼
ę“×ķ![]() Ż¼╦∙ęį
Ż¼╦∙ęį![]() .
.
╣╩į┌ŠĆČ╬![]() ╔Ž┤µį┌ę╗³c
╔Ž┤µį┌ę╗³c![]() Ż¼ØMūŃ
Ż¼ØMūŃ![]() Ż¼╩╣Č■├µĮŪ
Ż¼╩╣Č■├µĮŪ![]() Ą─ėÓŽęųĄ×ķ
Ą─ėÓŽęųĄ×ķ![]() .
.



| ─Ļ╝ē | Ė▀ųąšn│╠ | ─Ļ╝ē | │§ųąšn│╠ |
| Ė▀ę╗ | Ė▀ę╗├Ō┘Mšn│╠═Ų╦]ŻĪ | │§ę╗ | │§ę╗├Ō┘Mšn│╠═Ų╦]ŻĪ |
| Ė▀Č■ | Ė▀Č■├Ō┘Mšn│╠═Ų╦]ŻĪ | │§Č■ | │§Č■├Ō┘Mšn│╠═Ų╦]ŻĪ |
| Ė▀╚² | Ė▀╚²├Ō┘Mšn│╠═Ų╦]ŻĪ | │§╚² | │§╚²├Ō┘Mšn│╠═Ų╦]ŻĪ |
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐ęčų¬Æü╬’ŠĆ![]() Ą─Į╣³c×ķ
Ą─Į╣³c×ķ![]() Ż¼£╩ŠĆ×ķ
Ż¼£╩ŠĆ×ķ![]() Ż¼Æü╬’ŠĆ
Ż¼Æü╬’ŠĆ![]() ╔Ž┤µį┌ę╗³c
╔Ž┤µį┌ę╗³c![]() Ż¼▀^³c
Ż¼▀^³c![]() ū„
ū„![]() Ż¼┤╣ūŃ×ķ
Ż¼┤╣ūŃ×ķ![]() Ż¼╩╣
Ż¼╩╣![]() ╩ŪĄ╚▀ģ╚²ĮŪą╬Ūę├µĘe×ķ
╩ŪĄ╚▀ģ╚²ĮŪą╬Ūę├µĘe×ķ![]() .
.
Ż©1Ż®Ū¾Æü╬’ŠĆ![]() Ą─ĘĮ│╠Ż╗
Ą─ĘĮ│╠Ż╗
Ż©2Ż®╚¶³c![]() ╩ŪłA
╩ŪłA![]() ┼cÆü╬’ŠĆ
┼cÆü╬’ŠĆ![]() Ą─ę╗éĆĮ╗³cŻ¼³c
Ą─ę╗éĆĮ╗³cŻ¼³c![]() Ż¼«ö
Ż¼«ö![]() ╚ĪĄ├ūŅąĪųĄĢrŻ¼Ū¾┤╦ĢrłA
╚ĪĄ├ūŅąĪųĄĢrŻ¼Ū¾┤╦ĢrłA![]() Ą─ĘĮ│╠.
Ą─ĘĮ│╠.
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐į┌ų▒ĮŪū°ś╦ŽĄ![]() ųąŻ¼Ū·ŠĆ
ųąŻ¼Ū·ŠĆ![]() Ą─ģóöĄ(sh©┤)ĘĮ│╠×ķ
Ą─ģóöĄ(sh©┤)ĘĮ│╠×ķ![]() Ż©
Ż©![]() ×ķģóöĄ(sh©┤)Ż®Ż¼ęįū°ś╦įŁ³c
×ķģóöĄ(sh©┤)Ż®Ż¼ęįū°ś╦įŁ³c![]() ×ķśO³cŻ¼ęį
×ķśO³cŻ¼ęį![]() ▌Sš²░ļ▌S×ķśO▌SŻ¼Į©┴óśOū°ś╦ŽĄŻ©
▌Sš²░ļ▌S×ķśO▌SŻ¼Į©┴óśOū°ś╦ŽĄŻ©![]() Ż®Ż¼³c
Ż®Ż¼³c![]() ×ķŪ·ŠĆ
×ķŪ·ŠĆ![]() ╔ŽĄ─äė³cŻ¼³c
╔ŽĄ─äė³cŻ¼³c![]() į┌ŠĆČ╬
į┌ŠĆČ╬![]() Ą─čėķLŠĆ╔ŽŻ¼ŪęØMūŃ
Ą─čėķLŠĆ╔ŽŻ¼ŪęØMūŃ![]() Ż¼³c
Ż¼³c![]() Ą─▄ē█E×ķ
Ą─▄ē█E×ķ![]() ĪŻ
ĪŻ
Ż©ó±Ż®Ū¾![]() Ą─śOū°ś╦ĘĮ│╠Ż╗
Ą─śOū°ś╦ĘĮ│╠Ż╗
Ż©ó“Ż®įO³c![]() Ą─śOū°ś╦×ķ
Ą─śOū°ś╦×ķ![]() Ż¼Ū¾
Ż¼Ū¾![]() ├µĘeĄ─ūŅąĪųĄĪŻ
├µĘeĄ─ūŅąĪųĄĪŻ
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐ęčų¬║»öĄ(sh©┤)![]() .
.
Ż©ó±Ż®╚¶Ū·ŠĆ![]() į┌³c
į┌³c![]() ╠ÄĄ─ŪąŠĆ
╠ÄĄ─ŪąŠĆ![]() ┼cų▒ŠĆ
┼cų▒ŠĆ![]() ┤╣ų▒Ż¼Ū¾ŪąŠĆ
┤╣ų▒Ż¼Ū¾ŪąŠĆ![]() Ą─ĘĮ│╠Ż╗
Ą─ĘĮ│╠Ż╗
Ż©ó“Ż®╚¶![]() Ą─śO┤¾ųĄ║═śOąĪųĄĘųäe×ķ
Ą─śO┤¾ųĄ║═śOąĪųĄĘųäe×ķ![]() Ż¼
Ż¼![]() Ż¼ūC├„Ż║
Ż¼ūC├„Ż║![]() .
.
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐ęčų¬║»öĄ(sh©┤)![]() Ż«
Ż«
(1)ėæšō║»öĄ(sh©┤)![]() Ą─å╬š{(di©żo)ąįŻ╗
Ą─å╬š{(di©żo)ąįŻ╗
(2)╚¶║»öĄ(sh©┤)![]() ėąā╔éĆśOųĄ³c
ėąā╔éĆśOųĄ³c![]() Ż¼Ūę
Ż¼Ūę![]() ║Ń│╔┴óŻ¼Ū¾
║Ń│╔┴óŻ¼Ū¾![]() Ą─╚ĪųĄĘČć·Ż«
Ą─╚ĪųĄĘČć·Ż«
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐į┌ŲĮ├µų▒ĮŪū°ś╦ŽĄxOyųąŻ¼īóÖEłA![]() ╔Ž├┐ę╗³cĄ─ÖMū°ś╦▒Ż│ų▓╗ūāŻ¼┐vū°ś╦ūā?y©Łu)ķįŁüĒĄ─ę╗░ļŻ¼Ą├Ū·ŠĆCŻ¼ęįū°ś╦įŁ³c×ķśO³cŻ¼x▌Sš²░ļ▌S×ķśO▌SĮ©┴óśOū°ś╦ŽĄŻ¼ų▒ŠĆlĄ─śOū°ś╦ĘĮ│╠×ķ
╔Ž├┐ę╗³cĄ─ÖMū°ś╦▒Ż│ų▓╗ūāŻ¼┐vū°ś╦ūā?y©Łu)ķįŁüĒĄ─ę╗░ļŻ¼Ą├Ū·ŠĆCŻ¼ęįū°ś╦įŁ³c×ķśO³cŻ¼x▌Sš²░ļ▌S×ķśO▌SĮ©┴óśOū°ś╦ŽĄŻ¼ų▒ŠĆlĄ─śOū°ś╦ĘĮ│╠×ķ![]() Ż«
Ż«
![]() īæ│÷Ū·ŠĆCĄ─Ųš═©ĘĮ│╠║═ų▒ŠĆlĄ─ų▒ĮŪū°ś╦ĘĮ│╠Ż╗
īæ│÷Ū·ŠĆCĄ─Ųš═©ĘĮ│╠║═ų▒ŠĆlĄ─ų▒ĮŪū°ś╦ĘĮ│╠Ż╗
![]() ęčų¬³c
ęčų¬³c![]() Ūęų▒ŠĆl┼cŪ·ŠĆCĮ╗ė┌AĪóBā╔³cŻ¼Ū¾
Ūęų▒ŠĆl┼cŪ·ŠĆCĮ╗ė┌AĪóBā╔³cŻ¼Ū¾![]() Ą─ųĄŻ«
Ą─ųĄŻ«
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐ĻP(gu©Īn)ė┌![]() Ą─šfĘ©Ż¼š²┤_Ą─╩ŪŻ© Ż®
Ą─šfĘ©Ż¼š²┤_Ą─╩ŪŻ© Ż®
A.š╣ķ_╩ĮųąĄ─Č■ĒŚ╩ĮŽĄöĄ(sh©┤)ų«║═×ķ1024B.š╣ķ_╩ĮųąĄ┌6ĒŚĄ─Č■ĒŚ╩ĮŽĄöĄ(sh©┤)ūŅ┤¾
C.š╣ķ_╩ĮųąĄ┌5ĒŚ║═Ą┌7ĒŚĄ─Č■ĒŚ╩ĮŽĄöĄ(sh©┤)ūŅ┤¾D.š╣ķ_╩ĮųąĄ┌6ĒŚĄ─ŽĄöĄ(sh©┤)ūŅąĪ
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐─│ąŻį┌Ė▀Č■öĄ(sh©┤)īWĖé┘É│§┘É║¾Ż¼ī”90Ęų╝░ęį╔ŽĄ─│╔┐ā▀MąąĮy(t©»ng)ėŗŻ¼ŲõŅl┬╩Ęų▓╝ų▒ĘĮłD╚ńłD╦∙╩ŠŻ¼╚¶![]() ĘųöĄ(sh©┤)Č╬Ą─ģó┘ÉīW╔·╚╦öĄ(sh©┤)×ķ2.
ĘųöĄ(sh©┤)Č╬Ą─ģó┘ÉīW╔·╚╦öĄ(sh©┤)×ķ2.
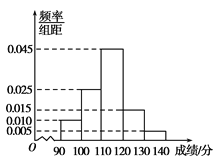
Ż©1Ż®Ū¾įōąŻ│╔┐āį┌![]() ĘųöĄ(sh©┤)Č╬Ą─ģó┘ÉīW╔·╚╦öĄ(sh©┤)Ż╗
ĘųöĄ(sh©┤)Č╬Ą─ģó┘ÉīW╔·╚╦öĄ(sh©┤)Ż╗
Ż©2Ż®╣└ėŗ90Ęų╝░ęį╔ŽĄ─īW╔·│╔┐āĄ─▒ŖöĄ(sh©┤)Īóųą╬╗öĄ(sh©┤)║═ŲĮŠ∙öĄ(sh©┤)Ż©ĮY(ji©”)╣¹▒Ż┴¶š¹öĄ(sh©┤)Ż®
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW üĒį┤Ż║ Ņ}ą═Ż║
ĪŠŅ}─┐Ī┐ęčų¬║»öĄ(sh©┤)![]() Ż©
Ż©![]() ╩Ūūį╚╗ī”öĄ(sh©┤)Ą─ĄūöĄ(sh©┤)Ż®Ż¼
╩Ūūį╚╗ī”öĄ(sh©┤)Ą─ĄūöĄ(sh©┤)Ż®Ż¼![]() .
.
Ż©1Ż®╚¶![]() Ż¼Ū¾
Ż¼Ū¾![]() Ą─śOųĄŻ╗
Ą─śOųĄŻ╗
Ż©2Ż®ī”╚╬ęŌ![]() Č╝ėą
Č╝ėą![]() │╔┴óŻ¼Ū¾īŹöĄ(sh©┤)
│╔┴óŻ¼Ū¾īŹöĄ(sh©┤)![]() Ą─╚ĪųĄĘČć·.
Ą─╚ĪųĄĘČć·.
Ż©3Ż®ī”╚╬ęŌ![]() ūC├„Ż║
ūC├„Ż║![]() Ż╗
Ż╗
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
ć°ļHīWąŻā×(y©Łu)▀x - ŠÜ┴Ģāį┴ą▒Ē - įćŅ}┴ą▒Ē
║■▒▒╩Ī╗ź┬ō(li©ón)ŠW(w©Żng)▀`Ę©║═▓╗┴╝ą┼Žó┼eł¾ŲĮ┼_ | ŠW(w©Żng)╔Žėą║”ą┼Žó┼eł¾īŻģ^(q©▒) | ļŖą┼įp“_┼eł¾īŻģ^(q©▒) | ╔µÜv╩Ę╠ō¤oų„┴xėą║”ą┼Žó┼eł¾īŻģ^(q©▒) | ╔µŲ¾ŪųÖÓ(qu©ón)┼eł¾īŻģ^(q©▒)
▀`Ę©║═▓╗┴╝ą┼Žó┼eł¾ļŖįÆŻ║027-86699610 ┼eł¾Ó]ŽõŻ║58377363@163.com