
【題目】甲、乙兩支籃球隊賽季總決賽采用7場4勝制,每場必須分出勝負,場與場之間互不影響,只要有一隊獲勝4場就結束比賽.現已比賽了4場,且甲籃球隊勝3場.已知甲球隊第5,6場獲勝的概率均為![]() ,但由于體力原因,第7場獲勝的概率為
,但由于體力原因,第7場獲勝的概率為![]() .
.
(1)求甲隊分別以![]() ,
,![]() 獲勝的概率;
獲勝的概率;
(2)設![]() 表示決出冠軍時比賽的場數,求
表示決出冠軍時比賽的場數,求![]() 的分布列及數學期望.
的分布列及數學期望.
 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:高中數學 來源: 題型:
【題目】在一個棱長為![]() 的正方體的表面涂上顏色,將其適當分割成棱長為
的正方體的表面涂上顏色,將其適當分割成棱長為![]() 的小正方體,全部放入不透明的口袋中,攪拌均勻后,從中任取一個,取出的小正方體表面僅有一個面涂有顏色的概率是()
的小正方體,全部放入不透明的口袋中,攪拌均勻后,從中任取一個,取出的小正方體表面僅有一個面涂有顏色的概率是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校在本校任選了一個班級,對全班50名學生進行了作業量的調查,根據調查結果統計后,得到如下的![]() 列聯表,已知在這50人中隨機抽取2人,這2人都“認為作業量大”的概率為
列聯表,已知在這50人中隨機抽取2人,這2人都“認為作業量大”的概率為![]() .
.
認為作業量大 | 認為作業量不大 | 合計 | |
男生 | 18 | ||
女生 | 17 | ||
合計 | 50 |
(1)請完成上面的列聯表;
(2)根據列聯表的數據,能否有![]() 的把握認為“認為作業量大”與“性別”有關?
的把握認為“認為作業量大”與“性別”有關?
附表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
附: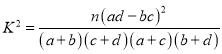 (其中
(其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】1,4,9,16……這些數可以用圖1中的點陣表示,古希臘畢達哥拉斯學派將其稱為正方形數,記第![]() 個數為
個數為![]() .在圖2的楊輝三角中,第
.在圖2的楊輝三角中,第![]() 行是
行是![]() 展開式的二項式系數
展開式的二項式系數![]() ,
,![]() ,…,
,…,![]() ,記楊輝三角的前
,記楊輝三角的前![]() 行所有數之和為
行所有數之和為![]() .
.

(1)求![]() 和
和![]() 的通項公式;
的通項公式;
(2)當![]() 時,比較
時,比較![]() 與
與![]() 的大小,并加以證明.
的大小,并加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代儒家要求學生掌握六種基本才藝:禮、樂、射、御、書、數,簡稱“六藝”,某高中學校為弘揚“六藝”的傳統文化,分別進行了主題為“禮、樂、射、御、書、數”六場傳統文化知識競賽,現有甲、乙、丙三位選手進入了前三名的最后角逐,規定:每場知識競賽前三名的得分都分別為![]()
![]() 且
且![]() ;選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為
;選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一場比賽中獲得第一名,下列說法正確的是( )
分,且乙在其中一場比賽中獲得第一名,下列說法正確的是( )
A. 乙有四場比賽獲得第三名
B. 每場比賽第一名得分![]() 為
為![]()
C. 甲可能有一場比賽獲得第二名
D. 丙可能有一場比賽獲得第一名
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知如下四個命題:①在線性回歸模型中,相關指數![]() 表示解釋變量
表示解釋變量![]() 對于預報變量
對于預報變量![]() 的貢獻率,
的貢獻率,![]() 越接近于
越接近于![]() ,表示回歸效果越好;②在回歸直線方程
,表示回歸效果越好;②在回歸直線方程![]() 中,當解釋變量
中,當解釋變量![]() 每增加一個單位時,預報變量
每增加一個單位時,預報變量![]() 平均增加
平均增加![]() 個單位;③兩個變量相關性越強,則相關系數的絕對值就越接近于
個單位;③兩個變量相關性越強,則相關系數的絕對值就越接近于![]() ;④對分類變量
;④對分類變量![]() 與
與![]() ,對它們的隨機變量
,對它們的隨機變量![]() 的觀測值
的觀測值![]() 來說,
來說,![]() 越小,則“
越小,則“![]() 與
與![]() 有關系”的把握程度越大.其中正確命題的序號是__________.
有關系”的把握程度越大.其中正確命題的序號是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》第八章“方程”問題八:今有賣牛二、羊五,以買十三豕,有余錢一千。賣牛三、豕三,以買九羊,錢適足.賣羊六、豕八,以買五牛,錢不足六百.問牛、羊、豕各幾何?“如果賣掉2頭牛和5只羊,可買13口豬,還余1000錢;賣掉3頭牛和3口豬的錢恰好可買9只羊;而賣掉6只羊和8口豬,去買5頭牛,還少600錢.問牛、羊、豬的價格各是多少”.按照題意,可解出牛______錢、羊______錢、豬______錢.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com