Question

【題目】已知函數(且)，

（1）若，且函數的值域為，求的解析式；

（2）在（1）的條件下，當時，時單調函數，求實數的取值范圍；

（3）當，時，若對于任意，不等式恒成立，求實數的取值范圍

Answer 1

【答案】（1）；（2）或；（3）.

【解析】

（1）由函數的值域為，得，再結合，從而求得的值，進而求得函數的解析式；

（2）函數的對稱軸不在區間內即可；

（3）將不等式恒成立轉化為不等式組對于任意，恒成立，看成以為主元，再分別研究兩個不等式恒成立問題.

（1）函數的值域為，所以，

又，所以，解得：

所以.

（2）因為，

對稱軸為，

所以或，解得：或.

（3）當時，，

因為，

所以不等式組對于任意，恒成立.

所以不等式組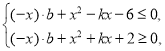對于任意，恒成立.

所以對于任意恒成立.

先考慮不等式對于任意恒成立，所以；

再考慮不等式對于任意恒成立（此時只考慮情況），

因為函數的對稱軸為，

①當時，不等式對于任意恒成立；

②當時，，則，

所以；

綜上所述：.