
【題目】【選做題】本題包括A、B、C、D四小題,請選定其中兩小題,并在相應的答題區域內作答.若多做,則按作答的前兩小題評分.解答時應寫出文字說明、證明過程或演算步驟.
A.[選修4-1:幾何證明選講]
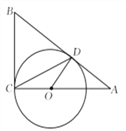
如圖, ![]() 分別與圓
分別與圓![]() 相切于點
相切于點![]() ,
, ![]() ,
, ![]() 經過圓心
經過圓心![]() ,且
,且![]() ,求證:
,求證: ![]() .
.
B.[選修4-2:矩陣與變換]
在平面直角坐標系中,已知點![]() ,
, ![]() ,
, ![]() ,
, ![]() ,先將正方形
,先將正方形![]() 繞原點
繞原點![]() 逆時針旋轉
逆時針旋轉![]() ,再將所得圖形的縱坐標壓縮為原來的一半、橫坐標不變,求連續兩次變換所對應的矩陣
,再將所得圖形的縱坐標壓縮為原來的一半、橫坐標不變,求連續兩次變換所對應的矩陣![]() .
.
C.[選修4-4:坐標系與參數方程]
在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).現以
為參數).現以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,建立極坐標系,求曲線
軸的正半軸為極軸,建立極坐標系,求曲線![]() 的極坐標方程.
的極坐標方程.
D.[選修4-5:不等式選講]
已知![]() 為互不相等的正實數,求證:
為互不相等的正實數,求證: ![]() .
.
【答案】見解析.
【解析】A.根據題意,可以考慮證明![]() ,又由
,又由![]() ,從而問題可得證;B.根據旋轉變換矩陣、伸縮變換矩陣以及矩陣乘法的定義進行運算,問題可得解;C.根據題意,以直角坐標系的原點為極點,以
,從而問題可得證;B.根據旋轉變換矩陣、伸縮變換矩陣以及矩陣乘法的定義進行運算,問題可得解;C.根據題意,以直角坐標系的原點為極點,以![]() 軸的正半軸為極軸建立極坐標系,再由參數方程經過消參得到一般方程,再由一般方程化為極坐標方程即可;D.根據題意,可考慮使用分析法進行證明即可.
軸的正半軸為極軸建立極坐標系,再由參數方程經過消參得到一般方程,再由一般方程化為極坐標方程即可;D.根據題意,可考慮使用分析法進行證明即可.
試題解析:A.解:易得![]() ,
,
又![]() ,
,
故![]() ,
,
所以![]() .
.
又![]() ,
,
故![]() .
.
B.解:設將正方形![]() 繞原點
繞原點![]() 逆時針旋轉
逆時針旋轉![]() 所對應的矩陣為
所對應的矩陣為![]() ,
,
則![]() .
.
設將所得圖形的縱坐標壓縮為原來的一半,橫坐標不變所對應的矩陣為![]() ,
,
則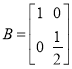 ,
,
所以連續兩次變換所對應的矩陣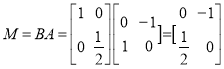 .
.
C.解:依題意知![]() (
(![]() 為參數),
為參數),
因為![]() ,
,
所以![]() ,即
,即![]() ,
,
化為極坐標方程得![]() ,即
,即![]() ,
,
所以曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
D.證明:因為![]() ,
, ![]() ,
,
所以要證![]() ,
,
只要證![]() ,
,
即要證![]() ,
,
只需證![]() ,
,
而![]() ,故
,故![]() 成立.
成立.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源: 題型:
【題目】已知集合![]() .對于
.對于![]() ,
, ![]() ,定義
,定義![]() 與
與![]() 之間的距離為
之間的距離為![]() .
.
(Ⅰ)寫出![]() 中的所有元素,并求兩元素間的距離的最大值;
中的所有元素,并求兩元素間的距離的最大值;
(Ⅱ)若集合![]() 滿足:
滿足: ![]() ,且任意兩元素間的距離均為2,求集合
,且任意兩元素間的距離均為2,求集合![]() 中元素個數的最大值并寫出此時的集合
中元素個數的最大值并寫出此時的集合![]() ;
;
(Ⅲ)設集合![]() ,
, ![]() 中有
中有![]() 個元素,記
個元素,記![]() 中所有兩元素間的距離的平均值為
中所有兩元素間的距離的平均值為![]() ,證明
,證明![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某校組織的“共筑中國夢”競賽活動中,甲、乙兩班各有6名選手參賽,在第一輪筆試環節中,評委將他們的筆試成績作為樣本數據,繪制成如圖所示的莖葉圖,為了增加結果的神秘感,主持人故意沒有給出甲、乙兩班最后一位選手的成績,只是告知大家,如果某位選手的成績高于90分(不含90分),則直接“晉級”.
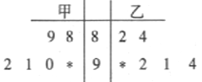
(1)求乙班總分超過甲班的概率;
(2)主持人最后宣布:甲班第六位選手的得分是90分,乙班第六位選手的得分是97分,
①請你從平均分和方差的角度來分析兩個班的選手的情況;
②主持人從甲乙兩班所有選手成績中分別隨機抽取2個,記抽取到“晉級”選手的總人數為![]() ,求
,求![]() 的分
的分
布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省電視臺為了解該省衛視一檔成語類節目的收視情況,抽查東西兩部各個城市,得到觀看該節目的人數(單位:千人),如莖葉圖所示,其中一個數字被污損.
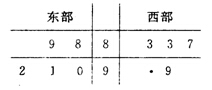
(1)求東部各城市觀看該節目觀眾平均人數超過西部各城市觀看該節目觀眾平均人數的概率;
(2)隨著節目的播出,極大激發了觀眾對成語知識學習積累的熱情,從中獲益匪淺.現從觀看該節目的觀眾中隨機統計了位觀眾的周均學習成語知識的時間(單位:小時)與年齡(單位:歲),并制作了對照表(如下表所示),
年齡x(歲) | ||||
周均學習成語知識時間y(小時) |
由表中數據,試求線性回歸方程,并預測年齡為歲觀眾周均學習成語知識時間.
參考公式: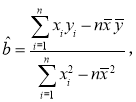 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某教研機構隨機抽取某校20個班級,調查各班關注漢字聽寫大賽的學生人數,根據所得數據的莖葉圖,以組距為5將數據分組成![]() 時,所作的頻率分布直方圖如圖所示,則原始莖葉圖可能是( )
時,所作的頻率分布直方圖如圖所示,則原始莖葉圖可能是( )
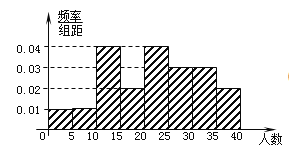
A.  B.
B. 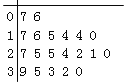
C. 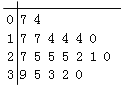 D.
D. 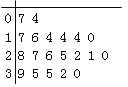
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() 滿足
滿足 ![]() (其中
(其中 ![]() ,
, ![]() ).
).
(1)求 ![]() 的表達式;
的表達式;
(2)對于函數 ![]() ,當
,當 ![]() 時,
時, ![]() ,求實數
,求實數 ![]() 的取值范圍.
的取值范圍.
(3)當 ![]() 時,
時, ![]() 的值為負數,求
的值為負數,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從2016年1月1日起全國統一實施全面兩孩政策. 為了解適齡民眾對放開
生二胎政策的態度,某市選取70后作為調查對象,隨機調查了10人,其中打算生二胎
的有4人,不打算生二胎的有6人.
(1)從這10人中隨機抽取3人,記打算生二胎的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(2)若以這10人的樣本數據估計該市的總體數據,且以頻率作為概率,從該市70后中隨機抽取3人,記打算生二胎的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com