【題目】對于任意的
，總存在
，使得
恒成立，則實數(shù)
的取值范圍是（ ）
A.
B.
C.
D.
【答案】A
【解析】
令
，根據(jù)題意得知：對任意的
，總存在
，使得
，則函數(shù)
在區(qū)間
上的最大值和最小值之差小于等于
，然后對實數(shù)
進(jìn)行分類討論，求得函數(shù)在區(qū)間上的最大值和最小值，可得出關(guān)于實數(shù)的不等式，進(jìn)而可求得實數(shù)的取值范圍.
令
，當(dāng)
時，
，
對任意的，總存在，使得，
由題意可知，函數(shù)在區(qū)間上的最大值和最小值之差小于等于.
（1）當(dāng)
時，即當(dāng)
時，函數(shù)在區(qū)間上單調(diào)遞增，
則
，
，所以，
，解得
，此時
；
（2）當(dāng)
時，即當(dāng)
時，函數(shù)在區(qū)間
上單調(diào)遞減，在區(qū)間
上單調(diào)遞增，
則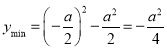
，由題意可得
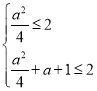，解得
，
此時；
（3）當(dāng)
時，即當(dāng)
時，函數(shù)在區(qū)間上單調(diào)遞減，
則
，
，則
，解得
，此時
.
綜上所述，實數(shù)的取值范圍是
.
故選：A.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】(2017安徽蚌埠一模)已知橢圓C:
=1(a>b>0)的離心率為
,F1,F2是橢圓的兩個焦點,P是橢圓上任意一點,且△PF1F2的周長是8+2
.
(1)求橢圓C的方程;
(2)設(shè)圓T:(x-2)2+y2=
,過橢圓的上頂點M作圓T的兩條切線交橢圓于E,F兩點,求直線EF的斜率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在三棱錐PABC中，不能證明AP⊥BC的條件是( )
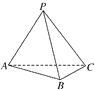
A. AP⊥PB，AP⊥PC
B. AP⊥PB，BC⊥PB
C. 平面BPC⊥平面APC，BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
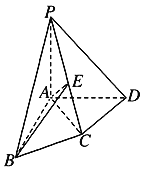
【題目】如圖，在四棱錐
中，PA⊥平面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中點．證明：
(1)CD⊥AE；
(2)PD⊥平面ABE.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖（1），在矩形
中，已知
分別為
和
的中點，對角線
與
交于
點，沿把矩形
折起，使兩個半平面所成二面角為60°，如圖（2）.
（1）求證：
；
（2）求
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】新鮮的荔枝很好吃，但摘下后容易變黑，影響賣相.某大型超市進(jìn)行扶貧工作，按計劃每年六月從精準(zhǔn)扶貧戶中訂購荔枝，每天進(jìn)貨量相同且每公斤20元，售價為每公斤24元，未售完的荔枝降價處理，以每公斤16元的價格當(dāng)天全部處理完.根據(jù)往年情況，每天需求量與當(dāng)天平均氣溫有關(guān).如果平均氣溫不低于25攝氏度，需求量為
公斤；如果平均氣溫位于
攝氏度，需求量為
公斤；如果平均氣溫位于
攝氏度，需求量為
公斤；如果平均氣溫低于15攝氏度，需求量為
公斤.為了確定6月1日到30日的訂購數(shù)量，統(tǒng)計了前三年6月1日到30日各天的平均氣溫數(shù)據(jù)，得到如圖所示的頻數(shù)分布表：
平均氣溫 |
|
|
|
|
|
|
天數(shù) | 2 | 16 | 36 | 25 | 7 | 4 |
（Ⅰ）假設(shè)該商場在這90天內(nèi)每天進(jìn)貨100公斤，求這90天荔枝每天為該商場帶來的平均利潤（結(jié)果取整數(shù)）；
（Ⅱ）若該商場每天進(jìn)貨量為200公斤，以這90天記錄的各需求量的頻率作為各需求量發(fā)生的概率，求當(dāng)天該商場不虧損的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某射擊手在同一條件下進(jìn)行射擊訓(xùn)練，結(jié)果如下：
射擊次數(shù)n | 10 | 20 | 50 | 100 | 200 | 500 |
擊中靶心次數(shù)m | 8 | 19 | 44 | 92 | 178 | 455 |
擊中靶心頻率 |
（1）求出表中擊中靶心的各個頻率值；
（2）這個射擊手射擊一次，擊中靶心的概率可估計為多少？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
．
（1）拋物線的開口向 、對稱軸為直線 、頂點坐標(biāo) ；
（2）當(dāng)
時，函數(shù)有最 值，是 ；
（3）當(dāng)
時，
隨的增大而增大；當(dāng) 時，隨的增大而減小；
（4）該函數(shù)圖象可由
的圖象經(jīng)過怎樣的平移得到的？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】選修4-4：坐標(biāo)系與參數(shù)方程
已知直線
的參數(shù)方程為
(
為參數(shù)),以坐標(biāo)原點為極點, 
軸的正半軸為極軸建立極坐標(biāo)系,圓
的極坐標(biāo)方程為
.
(I)求圓
的直角坐標(biāo)方程；
(II)若
是直線
與圓面
的公共點,求
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
