
【題目】如圖,三棱柱![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() .
.

(1)求證:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中數學 來源: 題型:
【題目】某學校一個生物興趣小組對學校的人工湖中養殖的某種魚類進行觀測研究,在飼料充足的前提下,興趣小組對飼養時間x(單位:月)與這種魚類的平均體重y(單位:千克)得到一組觀測值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)在給出的坐標系中,畫出關于x、y兩個相關變量的散點圖.
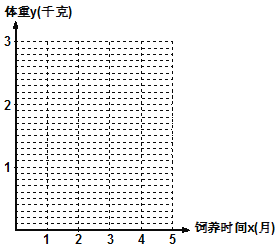
(2)請根據上表提供的數據,用最小二乘法求出變量![]() 關于變量
關于變量![]() 的線性回歸直線方程
的線性回歸直線方程![]() .
.
(3)預測飼養滿12個月時,這種魚的平均體重(單位:千克).
(參考公式: 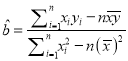 ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為奇函數,(1)求
為奇函數,(1)求![]() 的值;(2)判斷并證明函數
的值;(2)判斷并證明函數![]() 的單調性;(3)是否存在這樣的實數
的單調性;(3)是否存在這樣的實數![]() ,使
,使![]() 對一切
對一切![]() 恒成立,若存在,試求出
恒成立,若存在,試求出![]() 取值的集合;若不存在,說明理由.
取值的集合;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:
(單位: ![]() )和年利潤
)和年利潤![]() (單位:千元)的影響,對近8年的年宣傳費
(單位:千元)的影響,對近8年的年宣傳費![]() 和年銷售量
和年銷售量![]() 數據作了初步處理,得到下面的散點圖及一些統計量的值.
數據作了初步處理,得到下面的散點圖及一些統計量的值.


(1)根據散點圖判斷, ![]() 與
與![]() 哪一個適宜作為年銷售量
哪一個適宜作為年銷售量![]() 關于年宣傳費
關于年宣傳費![]() 的回歸方程類型?(給出判斷即可,不必說出理由);
的回歸方程類型?(給出判斷即可,不必說出理由);
(2)根據(1)的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)已知這種產品的年利潤![]() 與
與![]() 的關系為
的關系為![]() ,根據(2)的結果求:年宣傳費
,根據(2)的結果求:年宣傳費![]() 為何值時,年利潤最大?
為何值時,年利潤最大?
附:對于一組數據![]() ,
, ![]() ,…
,…![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某港口![]() 要將一件重要物品用小艇送到一艘正在航行的輪船上.在小艇出發時,輪船位于港口
要將一件重要物品用小艇送到一艘正在航行的輪船上.在小艇出發時,輪船位于港口![]() 北偏西
北偏西![]() 且與該港口相距20海里的
且與該港口相距20海里的![]() 處,并以30海里/時的航行速度沿正東方向勻速行駛,假設該小船沿直線方向以
處,并以30海里/時的航行速度沿正東方向勻速行駛,假設該小船沿直線方向以![]() 海里/時的航行速度勻速行駛,經過
海里/時的航行速度勻速行駛,經過![]() 小時與輪船相遇.
小時與輪船相遇.
(1)若希望相遇時小艇的航行距離最小,則小艇航行速度的大小應為多少?
(2)假設小艇的最高航行速度只能達到30海里/時,試設計航行方案(即確定航行方向與航行速度的大小),使得小艇能以最短時間與輪船相遇,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD-A1B1C1D中,M為DD1的中點,O為AC的中點,AB=2.

(I)求證:BD1∥平面ACM;
(Ⅱ)求證:B1O⊥平面ACM;
(Ⅲ)求三棱錐O-AB1M的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某次測驗中,有6位同學的平均成績為75分, 用xn表示編號為n(n=1,2,…,6)的同學所得成績,且前5位同學的成績如下:
編號n | 1 | 2 | 3 | 4 | 5 |
成績xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同學的成績x6,及這6位同學成績的標準差s;
(2)從前5位同學中選2位同學,求恰有1位同學成績在區間(68,75)中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com