
【題目】已知點![]() 在
在![]() 上,以R為切點的D的切線的斜率為
上,以R為切點的D的切線的斜率為![]() ,過
,過![]() 外一點A(不在x軸上)作
外一點A(不在x軸上)作![]() 的切線
的切線![]()
![]() ,點BC為切點,作平行于
,點BC為切點,作平行于![]() 的切線
的切線![]() (切點為D),點MN分別是與
(切點為D),點MN分別是與![]()
![]() 的交點(如圖).
的交點(如圖).
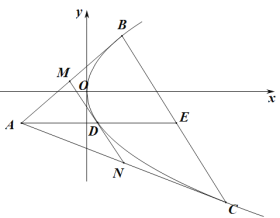
(1)用BC的縱坐標(biāo)st表示直線![]() 的斜率;
的斜率;
(2)設(shè)三角形![]() 面積為S,若將由過
面積為S,若將由過![]() 外一點的兩條切線及第三條切線(平行于兩切線切點的連線)圍成的三角形叫做“切線三角形”,如
外一點的兩條切線及第三條切線(平行于兩切線切點的連線)圍成的三角形叫做“切線三角形”,如![]() ,再由MN作“切線三角形”,并依這樣的方法不斷作切線三角形…,試?yán)?/span>“切線三角形”的面積和計算由拋物線及
,再由MN作“切線三角形”,并依這樣的方法不斷作切線三角形…,試?yán)?/span>“切線三角形”的面積和計算由拋物線及![]() 所圍成的陰影部分的面積T.
所圍成的陰影部分的面積T.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根據(jù)題意可知設(shè)出直線方程,由切線斜率的定義即可表示出直線![]() 的斜率;
的斜率;
(2)求得切線的斜率,可得D的坐標(biāo),求得直線![]() 的方程,運用中點坐標(biāo)公式可得A關(guān)于D的對稱點在直線
的方程,運用中點坐標(biāo)公式可得A關(guān)于D的對稱點在直線![]() 上,求得D為
上,求得D為![]() 的中點,根據(jù)
的中點,根據(jù)![]() 為三角形
為三角形![]() 的中位線,且E為
的中位線,且E為![]() 的中點,D為
的中點,D為![]() 的中點,求得三角形
的中點,求得三角形![]() 的面積,再由三角形的面積之比與對應(yīng)邊的比的關(guān)系,可得由拋物線外作出的“切線三角形”的面積構(gòu)成以
的面積,再由三角形的面積之比與對應(yīng)邊的比的關(guān)系,可得由拋物線外作出的“切線三角形”的面積構(gòu)成以![]() 為首項,
為首項,![]() 為公比的等比數(shù)列,運用無窮遞縮等比數(shù)列的求和公式,可得所有面積和,即可得到所求面積T.
為公比的等比數(shù)列,運用無窮遞縮等比數(shù)列的求和公式,可得所有面積和,即可得到所求面積T.
解:(1)設(shè)![]() 切線方程為
切線方程為![]() ,
,
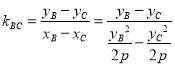 ,將B,C的縱坐標(biāo)代入得
,將B,C的縱坐標(biāo)代入得![]()
(2)設(shè)![]() ,則
,則![]() ,
,
∴![]() ,(s,t為B,C的縱坐標(biāo)),
,(s,t為B,C的縱坐標(biāo)),
![]() 由此可得
由此可得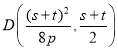
設(shè)![]() 利用切線方程得:
利用切線方程得:
 即
即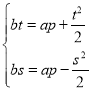 ,兩式相減得:
,兩式相減得:
![]() ,
,![]() ,
,![]() ,
,
由前面計算可知:![]() 平行于橫軸,可得
平行于橫軸,可得![]() ,
,
![]() ,將
,將![]() ,代入
,代入![]() ,
,
由![]() ,
,
所以D為![]() 的中點;
的中點;
設(shè):![]() ,由上可知
,由上可知![]() ,
,
由M,N確定的切線三角形的面積為![]() ,
,
后一個切線三角形的面積是前一切線三角形面積的![]() ,
,
由此繼續(xù)下去可得算式:
![]() ,
,
![]() ,
,
∴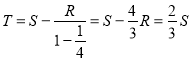 .
.


 暑假作業(yè)暑假快樂練西安出版社系列答案
暑假作業(yè)暑假快樂練西安出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,若在區(qū)間
,若在區(qū)間![]() 內(nèi)有且只有一個實數(shù)
內(nèi)有且只有一個實數(shù)![]() ,使得
,使得![]() 成立,則稱函數(shù)
成立,則稱函數(shù)![]() 在區(qū)間
在區(qū)間![]() 內(nèi)具有唯一零點.
內(nèi)具有唯一零點.
(1)判斷函數(shù)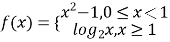 在區(qū)間
在區(qū)間![]() 內(nèi)是否具有唯一零點,說明理由:
內(nèi)是否具有唯一零點,說明理由:
(2)已知向量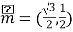 ,
,![]() ,
,![]() ,證明
,證明![]() 在區(qū)間
在區(qū)間![]() 內(nèi)具有唯一零點.
內(nèi)具有唯一零點.
(3)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 內(nèi)具有唯一零點,求實數(shù)
內(nèi)具有唯一零點,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() ,
,![]() .已知函數(shù)
.已知函數(shù)![]() ,
,![]() .
.
(Ⅰ)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)已知函數(shù)![]() 和
和![]() 的圖象在公共點(x0,y0)處有相同的切線,
的圖象在公共點(x0,y0)處有相同的切線,
(i)求證:![]() 在
在![]() 處的導(dǎo)數(shù)等于0;
處的導(dǎo)數(shù)等于0;
(ii)若關(guān)于x的不等式![]() 在區(qū)間
在區(qū)間![]() 上恒成立,求b的取值范圍.
上恒成立,求b的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有一容積為![]() 的正方體容器
的正方體容器![]() ,在棱
,在棱![]() 、
、![]() 和面對角線
和面對角線![]() 的中點各有一小孔
的中點各有一小孔![]() 、
、![]() 、
、![]() ,若此容器可以任意放置,則其可裝水的最大容積是( )
,若此容器可以任意放置,則其可裝水的最大容積是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某種“籠具”由內(nèi),外兩層組成,無下底面,內(nèi)層和外層分別是一個圓錐和圓柱,其中圓柱與圓錐的底面周長相等,圓柱有上底面,制作時需要將圓錐的頂端剪去,剪去部分和接頭忽略不計,已知圓柱的底面周長為![]() ,高為
,高為![]() ,圓錐的母線長為
,圓錐的母線長為![]() .
.
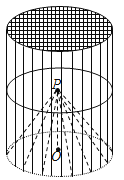
(1)求這種“籠具”的體積(結(jié)果精確到0.1![]() );
);
(2)現(xiàn)要使用一種紗網(wǎng)材料制作50個“籠具”,該材料的造價為每平方米8元,共需多少元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在下列命題中,正確的命題有________(填寫正確的序號)
①若![]() ,則
,則![]() 的最小值是6;
的最小值是6;
②如果不等式![]() 的解集是
的解集是![]() ,那么
,那么![]() 恒成立;
恒成立;
③設(shè)x,![]() ,且
,且![]() ,則
,則![]() 的最小值是
的最小值是![]() ;
;
④對于任意![]() ,
,![]() 恒成立,則t的取值范圍是
恒成立,則t的取值范圍是![]() ;
;
⑤“![]() ”是“復(fù)數(shù)
”是“復(fù)數(shù)![]() (
(![]() )是純虛數(shù)”的必要非充分條件;
)是純虛數(shù)”的必要非充分條件;
⑥若![]() ,
,![]() ,
,![]() ,則必有
,則必有![]() ;
;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
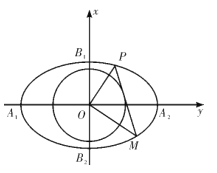
【題目】如圖,已知橢圓![]() 的左、右頂點為
的左、右頂點為![]() ,
,![]() ,上、下頂點為
,上、下頂點為![]() ,
,![]() ,記四邊形
,記四邊形![]() 的內(nèi)切圓為
的內(nèi)切圓為![]() .
.
(1)求圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)已知圓![]() 的一條不與坐標(biāo)軸平行的切線
的一條不與坐標(biāo)軸平行的切線![]() 交橢圓
交橢圓![]() 于P,M兩點.
于P,M兩點.
(i)求證:![]() ;
;
(ii)試探究![]() 是否為定值.
是否為定值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com