
【題目】設![]() ,
,![]() .已知函數
.已知函數![]() ,
,![]() .
.
(Ⅰ)求![]() 的單調區間;
的單調區間;
(Ⅱ)已知函數![]() 和
和![]() 的圖象在公共點(x0,y0)處有相同的切線,
的圖象在公共點(x0,y0)處有相同的切線,
(i)求證:![]() 在
在![]() 處的導數等于0;
處的導數等于0;
(ii)若關于x的不等式![]() 在區間
在區間![]() 上恒成立,求b的取值范圍.
上恒成立,求b的取值范圍.
【答案】(I)單調遞增區間為![]() ,
,![]() ,單調遞減區間為
,單調遞減區間為![]() .(II)(i)見解析.(ii)
.(II)(i)見解析.(ii)![]() .
.
【解析】
試題求導數后因式分解根據![]() ,得出
,得出![]() ,根據導數的符號判斷函數的單調性,給出單調區間,對
,根據導數的符號判斷函數的單調性,給出單調區間,對![]() 求導,根據函數
求導,根據函數![]() 和
和![]() 的圖象在公共點(x0,y0)處有相同的切線,解得
的圖象在公共點(x0,y0)處有相同的切線,解得![]() ,根據
,根據![]() 的單調性可知
的單調性可知![]() 在
在![]() 上恒成立,關于x的不等式
上恒成立,關于x的不等式![]() 在區間
在區間![]() 上恒成立,得出
上恒成立,得出![]() ,得
,得![]() ,
,![]() ,
,
求出![]() 的范圍,得出
的范圍,得出![]() 的范圍.
的范圍.
試題解析:(I)由![]() ,可得
,可得
![]() ,
,
令![]() ,解得
,解得![]() ,或
,或![]() .由
.由![]() ,得
,得![]() .
.
當![]() 變化時,
變化時,![]() ,
,![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
|
|
|
|
|
|
所以,![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,![]() ,單調遞減區間為
,單調遞減區間為![]() .
.
(II)(i)因為![]() ,由題意知
,由題意知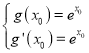 ,
,
所以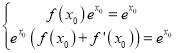 ,解得
,解得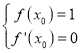 .
.
所以,![]() 在
在![]() 處的導數等于0.
處的導數等于0.
(ii)因為![]() ,
,![]() ,由
,由![]() ,可得
,可得![]() .
.
又因為![]() ,
,![]() ,故
,故![]() 為
為![]() 的極大值點,由(I)知
的極大值點,由(I)知![]() .
.
另一方面,由于![]() ,故
,故![]() ,
,
由(I)知![]() 在
在![]() 內單調遞增,在
內單調遞增,在![]() 內單調遞減,
內單調遞減,
故當![]() 時,
時,![]() 在
在![]() 上恒成立,從而
上恒成立,從而![]() 在
在![]() 上恒成立.
上恒成立.
由![]() ,得
,得![]() ,
,![]() .
.
令![]() ,
,![]() ,所以
,所以![]() ,
,
令![]() ,解得
,解得![]() (舍去),或
(舍去),或![]() .
.
因為![]() ,
,![]() ,
,![]() ,故
,故![]() 的值域為
的值域為![]() .
.
所以,![]() 的取值范圍是
的取值范圍是![]() .
.


 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:高中數學 來源: 題型:
【題目】如圖,有一張半徑為1米的圓形鐵皮,工人師傅需要剪一塊頂角為銳角的等腰三角形![]() ,不妨設
,不妨設 ![]() ,
, ![]() 邊上的高為
邊上的高為 ![]() ,圓心為
,圓心為 ![]() ,為了使三角形的面積最大,我們設計了兩種方案.
,為了使三角形的面積最大,我們設計了兩種方案.

(1)方案1:設 ![]() 為
為 ![]() ,用
,用![]() 表示
表示 ![]() 的面積
的面積 ![]() ; 方案2:設
; 方案2:設![]() 的高
的高![]() 為
為![]() ,用
,用![]() 表示
表示 ![]() 的面積
的面積![]() ;
;
(2)請從(1)中的兩種方案中選擇一種,求出![]() 面積的最大值
面積的最大值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某海輪以每小時30海里的速度航行,在點![]() 測得海面上油井
測得海面上油井![]() 在南偏東
在南偏東![]() ,海輪向北航行40分鐘后到達點
,海輪向北航行40分鐘后到達點![]() ,測得油井
,測得油井![]() 在南偏東
在南偏東![]() ,海輪改為北偏東
,海輪改為北偏東![]() 的航向再行駛80分鐘到達點
的航向再行駛80分鐘到達點![]() ,則
,則![]() 兩點的距離為(單位:海里)
兩點的距離為(單位:海里)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,![]() 底面ABC,
底面ABC,![]() .點D,E,N分別為棱PA,PC,BC的中點,M是線段AD的中點,
.點D,E,N分別為棱PA,PC,BC的中點,M是線段AD的中點,![]() ,
,![]() .
.
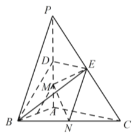
(1)求證:![]() 平面BDE;
平面BDE;
(2)求二面角C-EM-N的正弦值.
(3)已知點H在棱PA上,且直線NH與直線BE所成角的余弦值為![]() ,求線段AH的長.
,求線段AH的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 過點
過點 ,離心率為
,離心率為![]() .
.![]() 分別是橢圓
分別是橢圓![]() 的上、下頂點,
的上、下頂點,![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 的一點.
的一點.

(1)求橢圓![]() 的方程;
的方程;
(2)若點![]() 在直線
在直線![]() 上,且
上,且![]() ,求
,求![]() 的面積;
的面積;
(3)過點![]() 作斜率為
作斜率為![]() 的直線分別交橢圓
的直線分別交橢圓![]() 于另一點
于另一點![]() ,交
,交![]() 軸于點
軸于點![]() ,且點
,且點![]() 在線段
在線段![]() 上(不包括端點
上(不包括端點![]() ),直線
),直線![]() 與直線
與直線![]() 交于點
交于點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() :
:![]() ,
,![]() 為左、右焦點,
為左、右焦點,![]() 為短軸端點,且
為短軸端點,且![]() ,離心率為
,離心率為![]() ,
,![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程,
的方程,
(2)是否存在圓心在原點的圓,使得該圓的任意一條切線與橢圓C恒有兩個交點![]() ,
,![]() ,且滿足
,且滿足![]() ?若存在,求出該圓的方程,若不存在,說明理由.
?若存在,求出該圓的方程,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司利用簡單隨機抽樣方法,對投保車輛進行抽樣,樣本車輛中每輛車的賠付結果統計如下:
賠付金額(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
車輛數(輛) | 500 | 130 | 100 | 150 | 120 |
(1)若每輛車的投保金額均為2800元,估計賠付金額大于投保金額的概率.
(2)在樣本車輛中,車主是新司機的占10%,在賠付金額為4000元的樣本車輛中,車主是新司機的占20%,估計在已投保車輛中,新司機獲賠金額為4000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網站針對“2016年春節放假安排”開展網上問卷調查,提出了A,B兩種放假方案,調查結果如表:(單位:萬人)
人群 | 青少年 | 中年人 | 老年人 |
支持A方案 | 200 | 400 | 800 |
支持B方案 | 100 | 100 | n |
已知從所有參與調查的人中任選1人是“老年人”的概率為![]() .
.
(1)求n的值;
(2)從參與調查的“老年人”中,用分層抽樣的方法抽取6人,在這6人中任意選取2人,求恰好有1人“支持B方案”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數據![]() 是鄭州市普通職工
是鄭州市普通職工![]() 個人的年收入,若這
個人的年收入,若這![]() 個數據的中位數為
個數據的中位數為![]() ,平均數為
,平均數為![]() ,方差為
,方差為![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,則這
,則這![]() 個數據中,下列說法正確的是( )
個數據中,下列說法正確的是( )
A.年收入平均數大大增大,中位數一定變大,方差可能不變
B.年收入平均數大大增大,中位數可能不變,方差變大
C.年收入平均數大大增大,中位數可能不變,方差也不變
D.年收入平均數可能不變,中位數可能不變,方差可能不變
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com