
如圖,在三棱錐S ?ABC中,平面EFGH分別與BC,CA,AS,SB交于點E,F,G,H,且SA⊥平面EFGH,SA⊥AB,EF⊥FG.
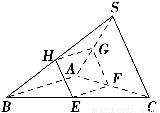
求證:(1)AB∥平面EFGH;
(2)GH∥EF;
(3)GH⊥平面SAC.
 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案 應用題作業本系列答案
應用題作業本系列答案科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練填空題押題練D組練習卷(解析版) 題型:填空題
已知函數f(x)=-xln x+ax在(0,e)上是增函數,函數g(x)=|ex-a|+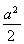 ,當x∈[0,ln 3]時,函數g(x)的最大值M與最小值m的差為
,當x∈[0,ln 3]時,函數g(x)的最大值M與最小值m的差為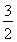 ,則a=________.
,則a=________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練倒數第9天練習卷(解析版) 題型:填空題
設函數f(x),g(x)的定義域分別為M,N,且M是N真子集,若對任意的x∈M,都有g(x)=f(x),則稱g(x)是f(x)的“拓展函數”.已知函數f(x)=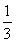 log2x,若g(x)是f(x)的“拓展函數”,且g(x)是偶函數,則符合條件的一個g(x)的解析式是________.
log2x,若g(x)是f(x)的“拓展函數”,且g(x)是偶函數,則符合條件的一個g(x)的解析式是________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練倒數第9天練習卷(解析版) 題型:填空題
已知函數y=f(x)的圖象在點M(1,f(1))處的切線方程是y= x+2,則f(1)+f′(1)=________.
x+2,則f(1)+f′(1)=________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練倒數第8天練習卷(解析版) 題型:填空題
設a,b為空間的兩條直線,α,β為空間的兩個平面,給出下列命題:
①若a∥α,a∥β,則α∥β;②若a⊥α,α⊥β,則α⊥β;
③若a∥α,b∥α,則a∥b; ④若a⊥α,b⊥α,則a∥b.
上述命題中,所有真命題的序號是________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練倒數第7天練習卷(解析版) 題型:填空題
已知二次函數f(x)=ax2-4x+c的值域是[0,+∞),則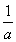 +
+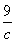 的最小值是________.
的最小值是________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練倒數第6天練習卷(解析版) 題型:填空題
已知函數f(x)=1-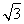 sin 2x+2cos2x,則函數y=f(x)的單調遞減區間為________.
sin 2x+2cos2x,則函數y=f(x)的單調遞減區間為________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練倒數第3天練習卷(解析版) 題型:解答題
在平面直角坐標系xOy中,直線x+y+2=0在矩陣M=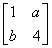 對應的變換作用下得到直線m:x-y-4=0,求實數a,b的值.
對應的變換作用下得到直線m:x-y-4=0,求實數a,b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com