
���}Ŀ����ֱ֪��(xi��n)l��y=3x+3��
��1�����c(di��n)P��5��3���P(gu��n)��ֱ��(xi��n)l�Č�(du��)�Q(ch��ng)�c(di��n)P�������(bi��o)��
��2����ֱ��(xi��n)l1��x��y��2=0�P(gu��n)��ֱ��(xi��n)l�Č�(du��)�Q(ch��ng)ֱ��(xi��n)l2�ķ��̣�
��3����֪�c(di��n)M��2��6����ԇ��ֱ��(xi��n)l����һ�c(di��n)Nʹ��|NP|+|NM|��ֵ��С��
���𰸡�
��1���⣺�O(sh��)�c(di��n)P�Č�(du��)�Q(ch��ng)�c(di��n)��P'��a��b����
�t 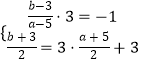 ����ã�
����ã� ![]() ��
��
���c(di��n)P'������(bi��o)�飨��4��6����
��2���⣺�ⷽ�̽M ![]() ��
�� 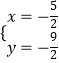 ��
��
����ֱ��(xi��n)l�cl�Ľ��c(di��n)����(bi��o)�� ![]()
��?y��n)�ֱ��(xi��n)l�cl2�P(gu��n)��ֱ��(xi��n)l��(du��)�Q(ch��ng)������ֱ��(xi��n)l2���^(gu��)�c(di��n) ![]() ��
��
���ɣ�1����֪���c(di��n)P��5��3��ǡ����ֱ��(xi��n)l�ϣ������P(gu��n)��ֱ��(xi��n)l�Č�(du��)�Q(ch��ng)�c(di��n)��P'����4��6����
����ֱ��(xi��n)l2���^(gu��)�c(di��n)P'����4��6�����@���Ƀ��c(di��n)ʽ�ɵã�  ��
��
��7x+y+22=0��
��3���⣺�ɣ�1����P'����4��6�����B��P'M����ֱ��(xi��n)l��N���B��NP��
�t|NP|+|NM|=|NP'|+|NM|=|P'M|����
�O(sh��)��N��x��3x+3�����t��P'��M��N����(xi��n)���ɵã�
![]() ����ã�x=1��
����ã�x=1��
�t�ɵ�N��1��6����
����������1���O(sh��)�c(di��n)P�Č�(du��)�Q(ch��ng)�c(di��n)��P'��a��b���������c(di��n)����(bi��o)��ʽ�̓�ֱ��(xi��n)��ֱ�ėl���з��̣�������ɣ���2�����������ֱ��(xi��n)�Ľ��c(di��n)�������c(di��n)�P(gu��n)��ֱ��(xi��n)��(du��)�Q(ch��ng)���������(du��)�Q(ch��ng)�c(di��n)������ֱ��(xi��n)���̵���ʽ�����ɵõ�����3�����ɣ�1���ĽY(ji��)Փ���B��P'M����ֱ��(xi��n)l��N���B��NP���������c(di��n)����(xi��n)��֪�R(sh��)���������N��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ������(sh��)
������(sh��)![]() ��.
��.
������(sh��)![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
����������(xi��n)![]() �cֱ��(xi��n)
�cֱ��(xi��n)![]() ���У��C����
�����C���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����˽ⴺ����ҹ�ز��С�c�N�Ӱl(f��)ѿ����֮�g���P(gu��n)ϵ���F(xi��n)��4�µ�30�����S�C(j��)���x��5���M(j��n)���о����ҷքeӛ���ÿ�앃ҹ�ز��cÿ��ÿ50�w�N�ӽ��ݺ�İl(f��)ѿ��(sh��)���õ����±���
���� | 4��1�� | 4��6�� | 4��12�� | 4��19�� | 4��27�� |
�ز� | 2 | 3 | 5 | 4 | 1 |
�l(f��)ѿ��(sh��) | 9 | 11 | 15 | 13 | 7 |
��1�����@5�������x2�죬ӛ�l(f��)ѿ�ķN�Ӕ�(sh��)�քe��![]() �����¼���
�����¼���![]() ��С��13���ĸ��ʣ�
��С��13���ĸ��ʣ�
��2����4��30�Օ�ҹ�ز��![]() ��Ո(q��ng)����(j��)
��Ո(q��ng)����(j��)![]() �P(gu��n)��
�P(gu��n)��![]() �ľ�(xi��n)�Իؚw����
�ľ�(xi��n)�Իؚw����![]() ��Ӌ(j��)ԓ��N�ӽ��ݺ�İl(f��)ѿ��(sh��).
��Ӌ(j��)ԓ��N�ӽ��ݺ�İl(f��)ѿ��(sh��).
������ʽ��  ��
�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����ֱ��(xi��n)a��b���ɽǞ�60�ȣ�A����gһ�c(di��n)���t�^(gu��)�c(di��n)A�ca��b����60�Ƚǵ�ֱ��(xi��n)�У� ���l��
A.4
B.3
C.2
D.1
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1�����C�����ڶ��c(di��n)![]() ��ʹ�ú���(sh��)
��ʹ�ú���(sh��)![]() �D��������һ�c(di��n)
�D��������һ�c(di��n)![]() �P(gu��n)��
�P(gu��n)��![]() �c(di��n)��(du��)�Q(ch��ng)���c(di��n)
�c(di��n)��(du��)�Q(ch��ng)���c(di��n)![]() Ҳ�ں���(sh��)
Ҳ�ں���(sh��)![]() �ĈD���ϣ�������c(di��n)
�ĈD���ϣ�������c(di��n)![]() ������(bi��o)��
������(bi��o)��
��2�����x![]() ������
������![]() ��
��![]() ����
����![]() ��
��
��3����(du��)�ڣ�2���е�![]() �����C����(du��)������
�����C����(du��)������![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����и�����(sh��)���䶨�x���У������溯��(sh��)������������(sh��)���ǣ� ��
A.y=x+1
B.y=��x3
C.y=�� ![]()
D.y=x|x|
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���������̼��(j��ng)��(j��)���(hu��)���ϲ����_(k��i)�����ô��(hu��)�ԡ���(ji��)�ܜp�ţ��Gɫ���B(t��i)�������}��ij��λ�ڇ�(gu��)�ҿ��в��T(m��n)��֧���£��M(j��n)�м��g(sh��)���P(gu��n)���������¹�ˇ���Ѷ�����̼�D(zhu��n)����һ�N�����õĻ����a(ch��n)Ʒ����֪ԓ��λÿ�µ�̎�������ٞ�300���������600������̎���ɱ�y��Ԫ���c��̎����x������֮�g�ĺ���(sh��)�P(gu��n)ϵ�ɽ��Ƶر�ʾ�� ![]() ����ÿ̎��һ��������̼�õ������õĻ����a(ch��n)Ʒ�r(ji��)ֵ��200Ԫ��
����ÿ̎��һ��������̼�õ������õĻ����a(ch��n)Ʒ�r(ji��)ֵ��200Ԫ��
��1��ԓ��λÿ��̎���������?l��i)��r(sh��)������ʹÿ����ƽ��̎���ɱ���ͣ�
��2��ԓ��λÿ���ܷ�@��������@��������������(r��n)��������@�����t��Ҫ��(gu��)�������a(b��)�N����Ԫ����ʹԓ��λ��̝�p��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����A={x| ![]() ��0��x��R}��B={x|x2��2x��m��0��x��R}
��0��x��R}��B={x|x2��2x��m��0��x��R}
��1����(d��ng)m=3�r(sh��)����A�ɣ�RB����
��2����A��B={x|��1��x��4}����(sh��)��(sh��)m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����������(xi��n)![]() ������һ�c(di��n)
������һ�c(di��n)![]() �����c(di��n)���о�(xi��n)
�����c(di��n)���о�(xi��n)![]() ������(xi��n)�Ͽ����ڮ���
������(xi��n)�Ͽ����ڮ���![]() ���c(di��n)
���c(di��n)![]() �����c(di��n)
�����c(di��n)![]() �����c(di��n)���о�(xi��n)
�����c(di��n)���о�(xi��n)![]() ����
����![]() ���t�Q(ch��ng)����(xi��n)
���t�Q(ch��ng)����(xi��n)![]() ���С���ƽ���ԡ����F(xi��n)���������}��
���С���ƽ���ԡ����F(xi��n)���������}��
�ٺ���(sh��)![]() �ĈD����С���ƽ���ԡ���
�ĈD����С���ƽ���ԡ���
�ڶ��x��![]() ���溯��(sh��)
���溯��(sh��)![]() �ĈD���С���ƽ���ԡ���
�ĈD���С���ƽ���ԡ���
�����κ���(sh��)![]() ���С���ƽ���ԡ����Ҍ�(du��)��(y��ng)�ă����c(di��n)
���С���ƽ���ԡ����Ҍ�(du��)��(y��ng)�ă����c(di��n)![]() ��
�� ![]() �ęM����(bi��o)�M(m��n)��
�ęM����(bi��o)�M(m��n)��![]() ��
��
��Ҫʹ�÷ֶκ���(sh��) �ĈD����С���ƽ���ԡ�����(d��ng)�҃H��(d��ng)
�ĈD����С���ƽ���ԡ�����(d��ng)�҃H��(d��ng)![]() .
.
��������}��(g��)��(sh��)����
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com