Question

【題目】選修4-4：坐標系與參數方程

在平面直角坐標系中，已知直線的參數方程為（為參數， 為傾斜角），以坐標原點為極點， 軸正半軸為極軸建立極坐標系，兩種坐標系中取相同的長度單位，曲線的極坐標方程為．

（Ⅰ）求曲線的普通方程和參數方程；

（Ⅱ）設與曲線交于， 兩點，求線段的取值范圍．

Answer 1

【答案】（Ⅰ）,（為參數）; （Ⅱ）.

【解析】試題分析:(1)根據,將曲線C的極坐標方程化為普通方程,進而寫出圓的參數方程;(2)將直線的參數方程代入曲線C中,整理并寫出韋達定理,根據t的幾何意義以及弦長公式表示出線段,根據三角函數的有界性求出取值范圍.

試題解析:（Ⅰ）因為曲線的極坐標方程為，

所以曲線的普通方程為，即，

所以曲線的參數方程為（為參數）．

（Ⅱ）把代入代入，

并整理得，

設， 對應的參數分別為， ，所以， ，

所以

，

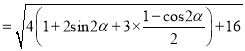
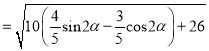設， ，∴，

∵，∴，∴，∴的取值范圍為．

點睛:把直角坐標系的原點作為極點,x軸的正半軸作為極軸,并在兩種坐標系中取相同的單位長度單位.設M是平面內任意一點,它的直角坐標為(x,y),極坐標是,則它們的關系是： .直線的參數方程中參數t的幾何意義是:t的絕對值等于直線上的動點M到定點P的距離.