
【題目】不等式![]() -kx+1≤0的解集非空,則k的取值范圍為________.
-kx+1≤0的解集非空,則k的取值范圍為________.
【答案】(-∞,-![]() ]∪[
]∪[![]() ,+∞)
,+∞)
【解析】由![]() -kx+1≤0,得
-kx+1≤0,得![]() ≤kx-1,設f(x)=
≤kx-1,設f(x)=![]() ,g(x)=kx-1,顯然函數f(x)和g(x)的定義域都為[-2,2].令y=
,g(x)=kx-1,顯然函數f(x)和g(x)的定義域都為[-2,2].令y=![]() ,兩邊平方得x2+y2=4,故函數f(x)的圖象是以原點O為圓心,2為半徑的圓在x軸上及其上方的部分.
,兩邊平方得x2+y2=4,故函數f(x)的圖象是以原點O為圓心,2為半徑的圓在x軸上及其上方的部分.
而函數g(x)的圖象是直線l:y=kx-1在[-2,2]內的部分,該直線過點C(0,-1),斜率為k.
如圖,作出函數f(x),g(x)的圖象,不等式的解集非空,即直線l和半圓有公共點,可知k的幾何意義就是半圓上的點與點C(0,-1)連線的斜率.
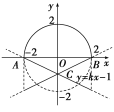
由圖可知A(-2,0),B(2,0),故kAC=ShadowSocks=-![]() ,kBC=
,kBC=![]() =
=![]() .
.
要使直線和半圓有公共點,則k≥![]() 或k≤-
或k≤-![]() .
.
所以k的取值范圍為(-∞,-![]() ]∪[
]∪[![]() ,+∞).
,+∞).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】有6名男醫生,4名女醫生.
(1)選3名男醫生,2名女醫生,讓這5名醫生到5個不同地區去巡回醫療,共有多少種不同方法?
(2)把10名醫生分成兩組,每組5人且每組都要有女醫生,則有多少種不同分法?若將這兩組醫生分派到兩地去,并且每組選出正副組長兩人,又有多少種不同方案?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 是定義在
是定義在![]() 上的偶函數,當
上的偶函數,當![]() 時,
時, ![]() ).
).
(1)當![]() 時,求
時,求![]() 的解析式;
的解析式;
(2)若![]() ,試判斷
,試判斷![]() 的上單調性,并證明你的結論;
的上單調性,并證明你的結論;
(3)是否存在![]() ,使得當
,使得當![]() 時,
時, ![]() 有最大值
有最大值![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面幾種推理是合情推理的是
①由圓的性質類比出球的有關性質;②由直角三角形、等腰三角形、等邊三角形的內角和是180°,歸納出所有三角形的內角和都是180°;③教室內有一把椅子壞了,則該教室內的所有椅子都壞了;④三角形內角和是180°,四邊形內角和是360°,五邊形內角和是540°,由此得出凸多邊形的內角和是(n-2)·180°___________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個結論:
(1)如果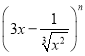 的展開式中各項系數之和為128,則展開式中
的展開式中各項系數之和為128,則展開式中![]() 的系數是-21;
的系數是-21;
(2)用相關指數![]() 來刻畫回歸效果,
來刻畫回歸效果, ![]() 的值越大,說明模型的擬合效果越差;
的值越大,說明模型的擬合效果越差;
(3)若![]() 是
是![]() 上的奇函數,且滿足
上的奇函數,且滿足![]() ,則
,則![]() 的圖象關于
的圖象關于![]() 對稱;
對稱;
(4)一個籃球運動員投籃一次得3分的概率為![]() ,得2分的概率為
,得2分的概率為![]() ,不得分的概率為
,不得分的概率為![]() ,且
,且![]() ,已知他投籃一次得分的數學期望為2,則
,已知他投籃一次得分的數學期望為2,則![]() 的最小值為
的最小值為![]() ;
;
其中正確結論的序號為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫藥研究所開發一種新藥,在試驗藥效時發現:如果成人按規定劑量服用,那么服藥后每毫升血液中的含藥量y(微克)與時間x(小時)之間滿足y= 其對應曲線(如圖所示)過點
其對應曲線(如圖所示)過點![]() .
.

(1)試求藥量峰值(y的最大值)與達峰時間(y取最大值時對應的x值);
(2)如果每毫升血液中含藥量不少于1微克時治療疾病有效,那么成人按規定劑量服用該藥后一次能維持多長的有效時間(精確到0.01小時)?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com