
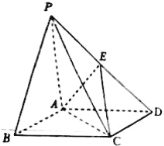
【題目】如圖,在四棱錐P—ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC,PB=PD=![]() AC,E是PD的中點,求證:
AC,E是PD的中點,求證:
(1)PB∥平面ACE;
(2)平面PAC⊥平面ABCD.
【答案】(1)見解析(2)見解析
【解析】
(1)連結BD,交AC于點O,連OE,根據底面圖像的特點得到O為BD的中點又E是PD的中點,故OE∥PB,進而得到線面平行;(2)根據底面ABCD是菱形,∠ABC=60°,所以![]() 為正三角形,通過邊長關系得到PB =
為正三角形,通過邊長關系得到PB =![]() AB =
AB =![]() PA,從而,PA⊥AB,同理可證PA⊥AD進而得到PA⊥平面ABCD,再由面面垂直的判定得到平面PAC⊥平面ABCD.
PA,從而,PA⊥AB,同理可證PA⊥AD進而得到PA⊥平面ABCD,再由面面垂直的判定得到平面PAC⊥平面ABCD.
(1)連結BD,交AC于點O,連OE.
因為底面ABCD是菱形,
所以點O為BD的中點.
又E是PD的中點,故OE∥PB.
又因為OE![]() 平面ACE,PB
平面ACE,PB![]() 平面ACE.
平面ACE.
(2)因為底面ABCD是菱形,∠ABC=60°,
所以![]() 為正三角形,從而AB = AC.
為正三角形,從而AB = AC.
又PB =![]() AC,PA = AC,
AC,PA = AC,
所以PB =![]() AB =
AB =![]() PA.
PA.
從而,PA⊥AB.
同理可證PA⊥AD,
又因為AB![]() AD = A,且AB,AD
AD = A,且AB,AD![]() 平面ABCD,
平面ABCD,
所以PA⊥平面ABCD.
因為PA![]() 平面PAC,所平面PAC⊥平面ABCD.
平面PAC,所平面PAC⊥平面ABCD.


科目:高中數學 來源: 題型:
【題目】某公司有男性職工64名,一次體檢后,將他們的體重(單位:kg)分組為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,繪制出頻率分布直方圖如圖,圖中從左到右的前3個小組的頻率之比為
,繪制出頻率分布直方圖如圖,圖中從左到右的前3個小組的頻率之比為![]() .
.

(1)求這64名男職工中,體重小于60kg的人數;
(2)從體重在![]() kg范圍的男職工中用分層抽樣的方法選取6名,再從這6名男職工中隨機選取2名,記“至少有一名男職工體重大于65kg”為事件
kg范圍的男職工中用分層抽樣的方法選取6名,再從這6名男職工中隨機選取2名,記“至少有一名男職工體重大于65kg”為事件![]() ,求事件
,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
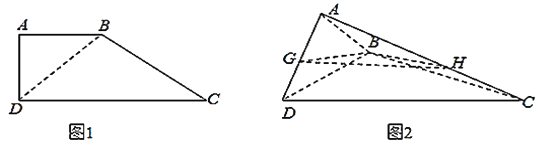
【題目】如圖![]() ,直角梯形
,直角梯形![]() ,
,![]() ,將
,將![]() 沿
沿![]() 折起來,使平面
折起來,使平面![]() 平面
平面![]() .如圖
.如圖![]() ,設
,設![]() 為
為![]() 的中點,
的中點,![]() ,
,![]() 的中點為
的中點為![]() .
.
(![]() )求證:
)求證:![]() 平面
平面![]() .
.
(![]() )求平面
)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
(![]() )在線段
)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ,若存在確定點
,若存在確定點![]() 的位置,若不存在,說明理由.
的位置,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正△ABC中,點D,E分別在邊AC, AB上,且AD=![]() AC,AE=
AC,AE=![]() AB,BD,CE相交于點F.
AB,BD,CE相交于點F.
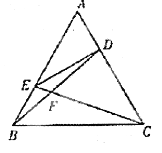
(Ⅰ)求證:A,E,F,D四點共圓;
(Ⅱ)若正△ABC的邊長為2,求A,E,F,D所在圓的半徑.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第23屆冬季奧運會于2018年2月9日至2月25日在韓國平昌舉行,期間正值我市學校放寒假,寒假結束后,某校工會對全校教職工在冬季奧運會期間每天收看比賽轉播的時間作了一次調查,得到如下頻數分布表:
收看時間(單位:小時) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) |
收看人數 | 14 | 30 | 16 | 28 | 20 | 12 |
(1)若將每天收看比賽轉播時間不低于3小時的教職工定義為“體育達人”,否則定義為“非體育達人”,請根據頻數分布表補全![]() 列聯表:
列聯表:
男 | 女 | 合計 | |
體育達人 | 40 | ||
非體育達人 | 30 | ||
合計 |
并判斷能否有90%的把握認為該校教職工是否為“體育達人”與“性別”有關;
(2)在全校“體育達人”中按性別分層抽樣抽取6名,再從這6名“體育達人”中選取2名作冬奧會知識講座.求抽取的這兩人恰好是一男一女的概率.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
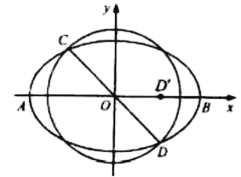
【題目】如圖,已知AB為橢圓E:![]() (a>b>0)的長軸,過坐標原點O且傾斜角為135°的直線交橢圓E于C,D兩點,且D在x軸上的射影D'恰為橢圓E的長半軸OB的中點.
(a>b>0)的長軸,過坐標原點O且傾斜角為135°的直線交橢圓E于C,D兩點,且D在x軸上的射影D'恰為橢圓E的長半軸OB的中點.
(1)求橢圓E的離心率;
(2)若AB=8,不過第四象限的直線l與橢圓E和以CD為直徑的圓均相切,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間為了規定工時定額,需要確定加工零件所花費的時間,為此作了四次試驗,得到的數據如下:
零件的個數 | 2 | 3 | 4 | 5 |
加工的時間 | 2.5 | 3 | 4 | 4.5 |
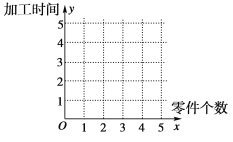
(1)在給定的坐標系中畫出表中數據的散點圖;
(2)求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并在坐標系中畫出回歸直線;
,并在坐標系中畫出回歸直線;
(3)試預測加工![]() 個零件需要多少時間?
個零件需要多少時間?
參考公式:回歸直線![]() ,其中
,其中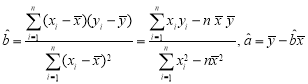 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某產品的三個質量指標分別為x, y, z, 用綜合指標S =" x" + y + z評價該產品的等級. 若S≤4, 則該產品為一等品. 現從一批該產品中, 隨機抽取10件產品作為樣本, 其質量指標列表如下:
產品編號 | A1 | A2 | A3 | A4 | A5 |
質量指標(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
產品編號 | A6 | A7 | A8 | A9 | A10 |
質量指標(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的樣本數據估計該批產品的一等品率;
(Ⅱ) 在該樣品的一等品中, 隨機抽取兩件產品,
(1) 用產品編號列出所有可能的結果;
(2) 設事件B為 “在取出的2件產品中, 每件產品的綜合指標S都等于4”, 求事件B發生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com