
(l2分)已知函數(shù) 為自然對數(shù)的底數(shù)
為自然對數(shù)的底數(shù)
(I) 當(dāng) 時,求函數(shù)
時,求函數(shù) 的極值;
的極值;
(Ⅱ) 若函數(shù) 在[-1,1]上單調(diào)遞減,求
在[-1,1]上單調(diào)遞減,求 的取值范圍.
的取值范圍.
解:(I)當(dāng) 時,
時, ,
, ………………2分
………………2分
當(dāng) 變化時,
變化時, ,
, 的變化情況如下表:
的變化情況如下表:
所以,當(dāng) 時,函數(shù)
時,函數(shù) 的極小值為
的極小值為 ,極大值為
,極大值為 .……………5分
.……………5分
(II)
令 ①若
①若 ,則
,則 ,在
,在 內(nèi),
內(nèi), ,即
,即 ,函數(shù)
,函數(shù) 在區(qū)間
在區(qū)間 上單調(diào)遞減.………………7分②若
上單調(diào)遞減.………………7分②若 ,則
,則 ,其圖象是開口向上的拋物線,對稱軸為
,其圖象是開口向上的拋物線,對稱軸為 ,當(dāng)且僅
,當(dāng)且僅
當(dāng) ,即
,即 時,在
時,在 內(nèi)
內(nèi) ,
, ,
,
函數(shù) 在區(qū)間
在區(qū)間 上單調(diào)遞減.………………9分
上單調(diào)遞減.………………9分
③若 ,則
,則 ,其圖象是開口向下的拋物線,
,其圖象是開口向下的拋物線,
當(dāng)且僅當(dāng) ,即
,即 時,在
時,在 內(nèi)
內(nèi) ,
, ,
,
函數(shù) 在區(qū)間
在區(qū)間 上單調(diào)遞減.………………………11分
上單調(diào)遞減.………………………11分
綜上所述,函數(shù) 在區(qū)間
在區(qū)間 上單調(diào)遞減時,
上單調(diào)遞減時, 的取值范圍是
的取值范圍是 .…12分
.…12分
解析


 同步練習(xí)西南大學(xué)出版社系列答案
同步練習(xí)西南大學(xué)出版社系列答案 補充習(xí)題江蘇系列答案
補充習(xí)題江蘇系列答案 學(xué)練快車道口算心算速算天天練系列答案
學(xué)練快車道口算心算速算天天練系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題12分)
已知二次函數(shù)
 (
(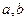 ,c為常數(shù)且1《c《4)的導(dǎo)函數(shù)的圖象如圖所示:
,c為常數(shù)且1《c《4)的導(dǎo)函數(shù)的圖象如圖所示:
( 1).求
1).求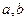 的值;
的值;
(2)記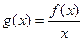 ,求
,求 在
在 上的最大值
上的最大值 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)已知函數(shù)f(x)=kx3-3(k+1)x2-2k2+4,若f(x)的單調(diào)減區(qū)間為(0,4 ).
).
(1)求k的值;
(2)對任意的t∈[-1,1],關(guān)于x的方程2x2+5x+a=f(t)總有實根,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分13分)已知函數(shù)
(I)求函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II)若
 ,在(1,2)上為單調(diào)遞
,在(1,2)上為單調(diào)遞
減函數(shù)。求實數(shù)a的范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分13分) 已知函數(shù) .
.
(Ⅰ)若函數(shù)在區(qū)間 其中a >0,上存在極
其中a >0,上存在極 值,求實數(shù)a的取值范
值,求實數(shù)a的取值范 圍;
圍;
(Ⅱ)如果當(dāng) 時,不等式
時,不等式 恒成立,求實數(shù)k的取值范圍;
恒成立,求實數(shù)k的取值范圍;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) ,其中
,其中
(1)若曲線
 在點
在點 處的切線方程為y=3x+1,求函數(shù)
處的切線方程為y=3x+1,求函數(shù) 的解析式;
的解析式;
(2)討論函數(shù) 的單調(diào)性;[來
的單調(diào)性;[來
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
已知函數(shù)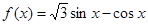 ,x∈R,若
,x∈R,若 ,則x的取值范圍為( ).
,則x的取值范圍為( ).
A.{x|kπ+ ≤x≤kπ+π,k∈Z} ≤x≤kπ+π,k∈Z} | B.{x|2kπ+ ≤x≤2kπ+π,k∈Z} ≤x≤2kπ+π,k∈Z} |
C.{x|kπ+ ≤x≤kπ+ ≤x≤kπ+ ,k∈Z} ,k∈Z} | D.{x|2kπ+ ≤x≤2kπ+ ≤x≤2kπ+ ,k∈Z} ,k∈Z} |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
已知 與
與 是定義在
是定義在 上的連續(xù)函數(shù),如果
上的連續(xù)函數(shù),如果 與
與 僅當(dāng)
僅當(dāng) 時的函數(shù)值為0,且
時的函數(shù)值為0,且 ,那么下列情形不可能出現(xiàn)的是( )
,那么下列情形不可能出現(xiàn)的是( )
A.0是 的極大值,也是 的極大值,也是 的極大值 的極大值 |
B.0是 的極小值,也是 的極小值,也是 的極小值 的極小值 |
C.0是 的極大值,但不是 的極大值,但不是 的極值 的極值 |
D.0是 的極小值,但不是 的極小值,但不是 的極值 的極值 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com