
���}Ŀ����ֱ֪��(xi��n)![]() �c���タ(xi��n)
�c���タ(xi��n)![]() ��
��![]() ����
����![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ����e��16��
����e��16��![]() ������(bi��o)ԭ�c(di��n)��.
������(bi��o)ԭ�c(di��n)��.
��1����![]() �ķ��̣�
�ķ��̣�
��2��ֱ��(xi��n)![]() ��(j��ng)�^(gu��)
��(j��ng)�^(gu��)![]() �Ľ��c(di��n)
�Ľ��c(di��n)![]() ��
��![]() ���c
���c![]() �S��ֱ���c
�S��ֱ���c![]() ����
����![]() ��
��![]() ���c(di��n)������(xi��n)��
���c(di��n)������(xi��n)��![]() �Ĵ�ֱƽ�־�(xi��n)�c
�Ĵ�ֱƽ�־�(xi��n)�c![]() �S�����c(di��n)
�S�����c(di��n)![]() ���C����
���C����![]() �鶨ֵ.
�鶨ֵ.
���𰸡���1��![]() ��2���C��Ҋ(ji��n)����
��2���C��Ҋ(ji��n)����
��������
��1����![]() ���뒁�タ(xi��n)�������
���뒁�タ(xi��n)�������![]() ���c(di��n)����(bi��o)������������e�����
���c(di��n)����(bi��o)������������e�����![]() ���Ò��タ(xi��n)���̣�
���Ò��タ(xi��n)���̣�
��2��ֱ���O(sh��)ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() �����뒁�タ(xi��n)���̣��O(sh��)
�����뒁�タ(xi��n)���̣��O(sh��)![]() ��
��![]() ���t�ɵ�
���t�ɵ�![]() ���ɽ��c(di��n)���L(zh��ng)��ʽ��
���ɽ��c(di��n)���L(zh��ng)��ʽ��![]() ��ͬ�r(sh��)�ɵ�
��ͬ�r(sh��)�ɵ�![]() ���c(di��n)����(bi��o)����(xi��)���д���(xi��n)���̣����
���c(di��n)����(bi��o)����(xi��)���д���(xi��n)���̣����![]() �c(di��n)����(bi��o)��
�c(di��n)����(bi��o)��![]() ��Ȼ�����ֵ
��Ȼ�����ֵ![]() �ɵã�
�ɵã�
��1���⣺��![]() ����
����![]() ����
����![]() ��
��
����![]() ����e��
����e��![]() .
.
��?y��n)?/span>![]() ������
������![]() ��
��
��![]() �ķ��̞�
�ķ��̞�![]() .
.
��2���C�������}���O(sh��)ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ��
��
��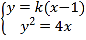 ����
����![]() .
.
�O(sh��)![]() ��
��![]() ���t
���t![]() ��
��
����![]() .
.
��?y��n)龀(xi��n)��![]() �����c(di��n)�ęM����(bi��o)��
�����c(di��n)�ęM����(bi��o)��![]() ���v����(bi��o)��
���v����(bi��o)��![]() ��
��
���Ծ�(xi��n)��![]() �Ĵ�ֱƽ�־�(xi��n)�ķ��̞�
�Ĵ�ֱƽ�־�(xi��n)�ķ��̞�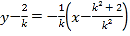 ��
��
��![]() ����
����![]() ������
������![]() �ęM����(bi��o)��
�ęM����(bi��o)��![]() ��
��
����![]() ��
��
��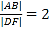 �鶨ֵ.
�鶨ֵ.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() �錍(sh��)��(sh��)����
�錍(sh��)��(sh��)����![]() ��ʾ�����^(gu��)
��ʾ�����^(gu��)![]() ���������(sh��)������
���������(sh��)������![]() ��
��![]() ��
��![]() .��(du��)�ں���(sh��)
.��(du��)�ں���(sh��)![]() ��������
��������![]() ��
��![]() ��ʹ��
��ʹ��![]() ���t�Q(ch��ng)����(sh��)
���t�Q(ch��ng)����(sh��)![]() �ǡ����C������(sh��).
�ǡ����C������(sh��).
��1���Дຯ��(sh��)![]() ��
��![]() �Ƿ��ǡ����C������(sh��)����ֻ�茑(xi��)���Y(ji��)Փ��
�Ƿ��ǡ����C������(sh��)����ֻ�茑(xi��)���Y(ji��)Փ��
��2���O(sh��)����(sh��)![]() �Ƕ��x��
�Ƕ��x��![]() �ϵ����ں���(sh��)������С���ڞ�
�ϵ����ں���(sh��)������С���ڞ�![]() ����
����![]() ���ǡ����C������(sh��)����
���ǡ����C������(sh��)����![]() ����Сֵ.
����Сֵ.
��3��������(sh��)![]() �ǡ����C������(sh��)����
�ǡ����C������(sh��)����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ijоƬ��˾��(du��)�������_(k��i)�l(f��)��һ��5G�֙C(j��)оƬ�M(j��n)�Мy(c��)�u(p��ng)��ԓ��˾�S�C(j��)�{(di��o)����100�wоƬ���������ýy(t��ng)Ӌ(j��)��(sh��)��(j��)�֞�![]() �傀(g��)С�M�����{(di��o)���оƬ�÷־���
�傀(g��)С�M�����{(di��o)���оƬ�÷־���![]() ��(n��i)�����õ���D��ʾ���l�ʷֲ�ֱ���D������
��(n��i)�����õ���D��ʾ���l�ʷֲ�ֱ���D������![]() ��
��
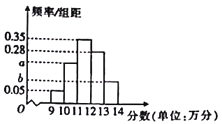
��1�����@100�wоƬ�u(p��ng)�y(c��)��?j��n)?sh��)��ƽ����(sh��)��ͬһ�M�е�ÿ��(g��)��(sh��)��(j��)����ԓ�M�^(q��)�g�����c(di��n)ֵ���棩��
��2��оƬ��˾���x100�wоƬ�����oij�֙C(j��)��˾�M(j��n)�Мy(c��)ԇ��ԓ�֙C(j��)��˾��ÿ�wоƬ�քe�b��3��(g��)�����֙C(j��)���M(j��n)�г��y(c��)����3��(g��)�����֙C(j��)���u(p��ng)�ֶ��_(d��)��11�f(w��n)�֣��t�J(r��n)��ԓоƬ�ϸ���3��(g��)�����֙C(j��)��ֻҪ��2��(g��)�u(p��ng)�֛](m��i)�_(d��)��11�f(w��n)�֣��t�J(r��n)��ԓоƬ���ϸ���3��(g��)�����֙C(j��)�ЃH1��(g��)�u(p��ng)�֛](m��i)���_(d��)��11�f(w��n)�֣��t��ԓоƬ�ٷքe��������2��(g��)�����֙C(j��)���M(j��n)�ж��y(c��)�����y(c��)�r(sh��)��2��(g��)�����֙C(j��)���u(p��ng)�ֶ��_(d��)��11�f(w��n)�֣��t�J(r��n)��ԓоƬ�ϸ�2��(g��)�����֙C(j��)��ֻҪ��1��(g��)�u(p��ng)�֛](m��i)�_(d��)��11�f(w��n)�֣��֙C(j��)��˾���J(r��n)��ԓоƬ���ϸ���֪ÿ�wоƬ�ڸ������ڹ����֙C(j��)�еĵ÷����(d��)��������оƬ��˾��(du��)оƬ���u(p��ng)�ַ�������(bi��o)��(zh��n)�c�֙C(j��)��˾��(du��)оƬ���u(p��ng)�ַ�������(bi��o)��(zh��n)��һ�£����l��������ʣ���ÿ�wоƬ����һ��(g��)�����֙C(j��)�еĜy(c��)ԇ�M(f��i)�þ���300Ԫ��ÿ�wоƬ�����J(r��n)����ϸ�ϸ������M(j��n)�к��m(x��)�y(c��)ԇ���F(xi��n)�֙C(j��)��˾�y(c��)ԇ���T(m��n)�A(y��)��Ĝy(c��)ԇ��(j��ng)�M(f��i)��10�f(w��n)Ԫ��ԇ��(w��n)�A(y��)�㽛(j��ng)�M(f��i)�Ƿ����y(c��)ԇ���@100�wоƬ��Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����֪�p����(xi��n)![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ��
��![]() ���^(gu��)�ҽ��c(di��n)��ƽ����һ�l�u����(xi��n)��ֱ��(xi��n)���p����(xi��n)���c(di��n)
���^(gu��)�ҽ��c(di��n)��ƽ����һ�l�u����(xi��n)��ֱ��(xi��n)���p����(xi��n)���c(di��n)![]() ����
����![]() �ă�(n��i)�ЈA�돽��
�ă�(n��i)�ЈA�돽��![]() ���t�p����(xi��n)���x���ʞ飨 ��
���t�p����(xi��n)���x���ʞ飨 ��
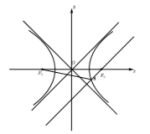
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij���S�ӹ�ij�N�����Ҫ��(j��ng)�^(gu��)![]() ��
��![]() ��
��![]() ����������ÿ������ļӹ������(d��)������������ӹ��ϸ�ĸ��ʷքe��
����������ÿ������ļӹ������(d��)������������ӹ��ϸ�ĸ��ʷքe��![]() ��
��![]() ��
��![]() .�������ϸ�������һ��(j��)Ʒ��ǡ�Ѓɵ�����ϸ����������(j��)Ʒ����������UƷ���Ҽӹ�һ��(g��)��������(j��)Ʒ�ĸ��ʞ�
.�������ϸ�������һ��(j��)Ʒ��ǡ�Ѓɵ�����ϸ����������(j��)Ʒ����������UƷ���Ҽӹ�һ��(g��)��������(j��)Ʒ�ĸ��ʞ�![]() .
.
��1����![]() ��
��
��2����ԓ�����һ��(j��)Ʒÿ��(g��)�ɫ@��200Ԫ������(j��)Ʒÿ��(g��)�ɫ@��100Ԫ��ÿ��(g��)�UƷ��ʹ���S�pʧ50Ԫ���O(sh��)һ��(g��)�����(j��ng)�^(gu��)��������ӹ�����K�@����![]() Ԫ����
Ԫ����![]() �ķֲ��м���(sh��)�W(xu��)����.
�ķֲ��м���(sh��)�W(xu��)����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������
^(q��)���@�����l(f��)չ���¼��g(sh��)�a(ch��n)�I(y��)�����M(j��n)���|(zh��)�����й�������(chu��ng)���Ʒ�|(zh��)����������O(sh��)�˾ӡ��˘I(y��)�����εġ����߾����¡�����ɽˮ�ǡ��Ŀ�Ը����ȫ���_(k��i)���r(sh��)������(m��ng)�롢������.���ľW(w��ng)�ѡ���������ͨ�^(gu��)��(w��n)������(du��)�������ο͝M(m��n)�������ǰ�����ą^(q��)��(n��i)���c(di��n)�M(j��n)���˽y(t��ng)Ӌ(j��)���Y(ji��)�����һ.����(j��)�˱�������(du��)���[�^(gu��)���T(m��n)���c(di��n)�ؑc��(d��ng)��@��100���ο��M(j��n)�НM(m��n)����{(di��o)�飬�o���c(di��n)��֣��M(m��n)�֞�100�֣��÷ֳ��^(gu��)90�ֵĞ顰�e�M(m��n)�⡱�������顰�����M(m��n)�⡱�������{(di��o)���ο����g��12�q�����µ���Ⱥ�Q(ch��ng)�郺ͯ���õ�![]() ��(li��n)�����������
��(li��n)�����������
��һ��
��ݾ��c(di��n)���� | 2014�� | 2015�� | 2016�� | 2017�� | 2018�� |
1 | �ؑc��(d��ng)��@ | �ؑc��(d��ng)��@ | ���T(m��n)ꇾ��^(q��) | ���ƺ� | ���ƺ� |
2 | �A�r���^(q��) | �A�r���^(q��) | �ؑc��(d��ng)��@�� | ���T(m��n)ꇾ��^(q��) | �S��ƺͿ�f�� |
3 | �͇�(gu��)�� | ���m���� | �S��ƺͿ�f�� | �A�r���^(q��) | �ؑc��(d��ng)��@ |
������
�e�M(m��n)�� | �����M(m��n)�� | ��Ӌ(j��) | |
��ͯ | 40 | ||
�ǃ�ͯ | 30 | ||
��Ӌ(j��) | 60 | 100 |
��1����ɱ�������(li��n)�������Д��Ƿ���99.9%�İ����J(r��n)���{(di��o)�錦(du��)���Ƿ��e�M(m��n)�⡱�c�Ƿ��ǃ�ͯ���P(gu��n)��
��2���鰲�Ź�(ji��)���ճ��У����������ı�һ��5��(g��)������S�C(j��)�x��2��(g��)��ݣ���?g��u)��@2��(g��)�������ǰ���ľ��c(di��n)�������x��1��(g��)���c(di��n)��ӛ�x����ľ��c(di��n)�С��ؑc��(d��ng)��@�����F(xi��n)�ĴΔ�(sh��)��![]() ����
����![]() �ķֲ��м���(sh��)�W(xu��)����
�ķֲ��м���(sh��)�W(xu��)����![]() .
.
������ʽ![]() .
.
������(sh��)��(j��)��![]() ��
��![]() ��
��![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ,
,![]() ,�t�����f(shu��)�����e(cu��)�`���ǣ� ��
,�t�����f(shu��)�����e(cu��)�`���ǣ� ��
A.![]() ��
��![]() ��(g��)���c(di��n)B.
��(g��)���c(di��n)B.![]() ��Сֵ��
��Сֵ��![]()
C.![]() �څ^(q��)�g
�څ^(q��)�g![]() ���{(di��o)�f�pD.
���{(di��o)�f�pD.![]() �ĈD���P(gu��n)��
�ĈD���P(gu��n)��![]() �S��(du��)�Q(ch��ng)
�S��(du��)�Q(ch��ng)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�ɶ��c(di��n)![]() ��
��![]() ���c(di��n)P�M(m��n)��
���c(di��n)P�M(m��n)��![]() .
.
��1�����c(di��n)P��܉�EC�ķ��̣�
��2����![]() ��ֱ��(xi��n)l�c܉�EC����A��B���c(di��n)��
��ֱ��(xi��n)l�c܉�EC����A��B���c(di��n)��![]() ��
��![]() ��б��֮�͞�2����(w��n)ֱ��(xi��n)l�Ƿ���^(gu��)���c(di��n)�����^(gu��)���c(di��n)��������c(di��n)������(bi��o)�������^(gu��)���c(di��n)��Ո(q��ng)�f(shu��)������.
��б��֮�͞�2����(w��n)ֱ��(xi��n)l�Ƿ���^(gu��)���c(di��n)�����^(gu��)���c(di��n)��������c(di��n)������(bi��o)�������^(gu��)���c(di��n)��Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У�ֱ��(xi��n)
�У�ֱ��(xi��n)![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)��.������(bi��o)ԭ�c(di��n)��O�c(di��n)��
�酢��(sh��)��.������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�ķ�ؓ(f��)���S��O�S��ȡ��ͬ�Ć�λ�L(zh��ng)�Ƚ����O����(bi��o)ϵ������(xi��n)
�S�ķ�ؓ(f��)���S��O�S��ȡ��ͬ�Ć�λ�L(zh��ng)�Ƚ����O����(bi��o)ϵ������(xi��n)![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��1����ֱ��(xi��n)![]() ����ͨ���̺�����(xi��n)
����ͨ���̺�����(xi��n)![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2���O(sh��)![]() ������(xi��n)
������(xi��n)![]() ������һ�c(di��n)��ֱ��(xi��n)
������һ�c(di��n)��ֱ��(xi��n)![]() �c������(bi��o)�S�Ľ��c(di��n)�քe��
�c������(bi��o)�S�Ľ��c(di��n)�քe��![]() ����
����![]() ���ֵ.
���ֵ.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com