
【題目】已知 ![]() ,方程f(x)=0有3個不同的根.
,方程f(x)=0有3個不同的根.
(1)求實數m的取值范圍;
(2)是否存在實數m,使得f(x)在(0,1)上恰有兩個極值點x1 , x2且滿足x2=2x1 , 若存在,求實數m的值;若不存在,說明理由.
【答案】
(1)解:由f(x)=0得: ![]() 或ln(x2+1﹣m)=0,
或ln(x2+1﹣m)=0,
可得 ![]() 或
或 ![]() ,
,
方程f(x)=0有3個不同的根,
從而0<m<1;
(2)解:由(1)得:0<m<1,
f′(x)=(3x2﹣m)ln(x2+1﹣m)+ ![]() ,
,
令x2=t,設 ![]() ,
,
∴g(0)=﹣mln(1﹣m)>0,∵0<m<1,
∴2﹣m>1,∴g(1)>0.g(a)=0,
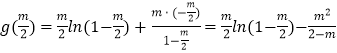 ,
,
∵0<m<1,∴g( ![]() )<0
)<0
∴存在t1∈(0, ![]() ),使得g(t1)=0,另外有m∈(
),使得g(t1)=0,另外有m∈( ![]() ,1),使得g(a)=0
,1),使得g(a)=0
假設存在實數m,使得f(x)在(0,1)上恰有兩個極值點x1,x2,且滿足x2=2x1,
則存在x1∈(0, ![]() ),使得f′(x1)=0,另外有f′(
),使得f′(x1)=0,另外有f′( ![]() )=0,即x2=
)=0,即x2= ![]() ,
,
∴x1= ![]() ,∴f′(
,∴f′( ![]() )=0,即(1﹣
)=0,即(1﹣ ![]() m)ln(1﹣
m)ln(1﹣ ![]() m)+
m)+ ![]() m=0 (*)
m=0 (*)
設h(m)=(1﹣ ![]() m)ln(1﹣
m)ln(1﹣ ![]() m)+
m)+ ![]() m,
m,
∴h′(a)=﹣ ![]() mln(1﹣
mln(1﹣ ![]() m)+
m)+ ![]() ,
,
∵0<m<1,∴h′(m)>0,
∴h(m)在(0,1)上是增函數
∴h(m)>h(0)=0
∴方程(*)無解,
即不存在實數m,使得f(x)在(0,1)上恰有兩個極值點x1,x2,且滿足x2=2x1.
【解析】(1)根據f(x)=0,得到關于m的不等式,解出m的范圍即可;(2)求導數,換元,存在t1∈(0, ![]() ),使得g(t1)=0,另外有m∈(
),使得g(t1)=0,另外有m∈( ![]() ,1),使得g(m)=0,再利用反證法,即可得出結論.
,1),使得g(m)=0,再利用反證法,即可得出結論.
【考點精析】通過靈活運用函數的極值與導數,掌握求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值即可以解答此題.
是極小值即可以解答此題.


 口算題天天練系列答案
口算題天天練系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 上的點到它的兩個焦的距離之和為
上的點到它的兩個焦的距離之和為![]() ,以橢圓
,以橢圓![]() 的短軸為直徑的圓
的短軸為直徑的圓![]() 經過這兩個焦點,點
經過這兩個焦點,點![]() ,
, ![]() 分別是橢圓
分別是橢圓![]() 的左、右頂點.
的左、右頂點.
(![]() )求圓
)求圓![]() 和橢圓
和橢圓![]() 的方程.
的方程.
(![]() )已知
)已知![]() ,
, ![]() 分別是橢圓
分別是橢圓![]() 和圓
和圓![]() 上的動點(
上的動點(![]() ,
, ![]() 位于
位于![]() 軸兩側),且直線
軸兩側),且直線![]() 與
與![]() 軸平行,直線
軸平行,直線![]() ,
, ![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,
, ![]() .求證:
.求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種出口產品的關稅稅率![]() ,市場價格
,市場價格![]() (單位:千元)與市場供應量
(單位:千元)與市場供應量![]() (單位:萬件)之間近似滿足關系式:
(單位:萬件)之間近似滿足關系式:![]() ,其中
,其中![]() 、
、![]() 均為常數.當關稅稅率為
均為常數.當關稅稅率為![]() 時,若市場價格為5千元,則市場供應量約為1萬件;當關稅稅率為
時,若市場價格為5千元,則市場供應量約為1萬件;當關稅稅率為![]() 時,若市場價格為7千元,則市場供應量約為2萬件.
時,若市場價格為7千元,則市場供應量約為2萬件.
(1)試確定![]() 、
、![]() 的值;
的值;
(2)市場需求量![]() (單位:萬件)與市場價格
(單位:萬件)與市場價格![]() 近似滿足關系式:
近似滿足關系式:![]() .當
.當![]() 時,市場價格稱為市場平衡價格.當市場平衡價格不超過4千元時,試確定關稅稅率的最大值.
時,市場價格稱為市場平衡價格.當市場平衡價格不超過4千元時,試確定關稅稅率的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=﹣1,|an﹣an﹣1|=2n﹣1(n∈N,n≥2),且{a2n﹣1}是遞減數列,{a2n}是遞增數列,則a2016= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在斜三棱柱ABC﹣A1B1C1中,側面ACC1A1與側面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2. 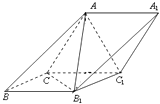
(1)求證:AB1⊥CC1;
(2)若 ![]() ,求二面角C﹣AB1﹣A1的正弦值.
,求二面角C﹣AB1﹣A1的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線AB為圓的切線,切點為B,點C在圓上,∠ABC的角平分線BE交圓于點E,DB垂直BE交圓于點D. 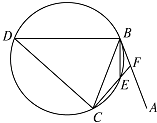
(1)證明:DB=DC;
(2)設圓的半徑為1,BC=3,延長CE交AB于點F,求△BCF外接圓的半徑.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某房地產開發公司計劃在一樓區內建造一個長方形公園ABCD,公園由形狀為長方形A1B1C1D1的休閑區和環公園人行道(陰影部分)組成.已知休閑區A1B1C1D1的面積為4000平方米,人行道的寬分別為4米和10米(如圖所示).

(1)若設休閑區的長和寬的比![]() =x(x>1),求公園ABCD所占面積S關于x的函數S(x)的解析式;
=x(x>1),求公園ABCD所占面積S關于x的函數S(x)的解析式;
(2)要使公園所占面積最小,則休閑區A1B1C1D1的長和寬該如何設計?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(Ⅰ)若函數![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求
,求![]() 的值;
的值;
(Ⅱ)當![]() 時,若不等式
時,若不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(Ⅲ)當![]() 時,若方程
時,若方程![]() 在
在![]() 上總有兩個不等的實根, 求
上總有兩個不等的實根, 求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com