
【題目】已知函數(shù)![]()
(1)若![]() ,證明:
,證明:![]() ;
;
(2)若![]() ,且
,且![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,且方程
,且方程![]() 有
有![]() 個不同的根,求
個不同的根,求![]() 的取值范圍.
的取值范圍.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由![]() ,可得
,可得![]() ,將等式兩邊分別代入解析式即可證明.
,將等式兩邊分別代入解析式即可證明.
(2)根據(jù)題意可得函數(shù)為增函數(shù),只需![]() 在
在![]() 恒成立,分離參數(shù)即可求解.
恒成立,分離參數(shù)即可求解.
(3)利用導(dǎo)數(shù)確定函數(shù)![]() 的單調(diào)區(qū)間,作出函數(shù)
的單調(diào)區(qū)間,作出函數(shù)![]() 的大致圖像,數(shù)形結(jié)合即可求解.
的大致圖像,數(shù)形結(jié)合即可求解.
(1)當(dāng)![]() 時,則
時,則![]() ,
,
所以左邊![]() ,
,
右邊![]()
![]() ,即證.
,即證.
(2)由![]() ,
,![]() ,
,
則函數(shù)![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
即![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,只需
上恒成立,只需![]() ,
,
設(shè)![]() ,由
,由![]() ,所以
,所以![]() ,
,
所以![]() .
.
(3)當(dāng)![]() 時,
時,![]()
則![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() ;
;
令![]() ,解得
,解得![]() ,
,
所以函數(shù)![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() ,
,![]() ,
,
函數(shù)![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,
,
且![]() ,
,![]() ,
,
在同一坐標(biāo)系中作出![]() 與
與![]() 的圖像如圖所示:
的圖像如圖所示:

方程![]() 有
有![]() 個不同的根,由圖像可知:
個不同的根,由圖像可知:![]()


 中考解讀考點(diǎn)精練系列答案
中考解讀考點(diǎn)精練系列答案 各地期末復(fù)習(xí)特訓(xùn)卷系列答案
各地期末復(fù)習(xí)特訓(xùn)卷系列答案 小博士期末闖關(guān)100分系列答案
小博士期末闖關(guān)100分系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年揚(yáng)州市政府打算在如圖所示的某“葫蘆”形花壇中建一噴泉,該花壇的邊界是兩個半徑為12米的圓弧圍成,兩圓心![]() 、
、![]() 之間的距離為
之間的距離為![]() 米.在花壇中建矩形噴泉,四個頂點(diǎn)
米.在花壇中建矩形噴泉,四個頂點(diǎn)![]() ,
,![]() ,
,![]() ,
,![]() 均在圓弧上,
均在圓弧上,![]() 于點(diǎn)
于點(diǎn)![]() .設(shè)
.設(shè)![]() .
.

![]() 當(dāng)
當(dāng) ![]() 時,求噴泉
時,求噴泉![]() 的面積
的面積![]() ;
;
(2)求![]() 為何值時,可使噴泉
為何值時,可使噴泉![]() 的面積
的面積![]() 最大?.
最大?.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() //
// ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).

(1)求證: ![]() ;
;
(2)求證: ![]() //平面
//平面![]() ;
;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】三角形的面積為![]() ,其中
,其中![]() ,
,![]() ,
,![]() 為三角形的邊長,
為三角形的邊長,![]() 為三角形內(nèi)切圓的半徑,則利用類比推理,可得出四面體的體積為( )
為三角形內(nèi)切圓的半徑,則利用類比推理,可得出四面體的體積為( )
A. ![]()
B. ![]()
C. ![]() ,(
,(![]() 為四面體的高)
為四面體的高)
D. ![]() ,(
,(![]() ,
,![]() ,
,![]() ,
,![]() 分別為四面體的四個面的面積,
分別為四面體的四個面的面積,![]() 為四面體內(nèi)切球的半徑)
為四面體內(nèi)切球的半徑)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
![]() .
.
(1)當(dāng)![]() 時,若函數(shù)
時,若函數(shù)![]() 恰有一個零點(diǎn),求
恰有一個零點(diǎn),求![]() 的取值范圍;
的取值范圍;
(2)當(dāng)![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出如圖數(shù)陣的表格形式,表格內(nèi)是按某種規(guī)律排列成的有限個正整數(shù).

(1)記第一行的自左至右構(gòu)成數(shù)列![]() ,
,![]() 是
是![]() 的前
的前![]() 項和,試求
項和,試求![]() 的表達(dá)式;
的表達(dá)式;
(2)記![]() 為第
為第![]() 行與第
行與第![]() 列交點(diǎn)的數(shù)字,觀察數(shù)陣,若
列交點(diǎn)的數(shù)字,觀察數(shù)陣,若![]() ,試求出
,試求出![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
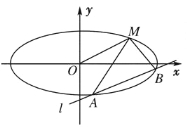
【題目】如圖,已知橢圓的中心在原點(diǎn),焦點(diǎn)在![]() 軸上,長軸長是短軸長的2倍且經(jīng)過點(diǎn)
軸上,長軸長是短軸長的2倍且經(jīng)過點(diǎn)![]() ,平行于
,平行于![]() 的直線
的直線![]() 在
在![]() 軸上的截距為
軸上的截距為![]() ,直線
,直線![]() 交橢圓于
交橢圓于![]() 兩個不同點(diǎn).
兩個不同點(diǎn).
(1)求橢圓的方程;
(2)求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,其中
,其中![]() .
.
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)設(shè)函數(shù)![]() ,當(dāng)
,當(dāng)![]() 時,若
時,若![]() ,
,![]() ,總有
,總有![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com