若數列
滿足條件：存在正整數
，使得
對一切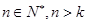
都成立，則稱數列為級等差數列．
（1）已知數列為2級等差數列，且前四項分別為
，求
的值；
（2）若
為常數），且是
級等差數列，求
所有可能值的集合，并求取最小正值時數列的前3
項和
；
（3）若既是
級等差數列，也是級等差數列，證明：是等差數列．
（1）19，（2）
，（3）詳見解析.
解析試題分析：（1）解新定義數列問題，關鍵從定義出發，建立等量關系.
，
（2）本題化簡是關鍵.因為是級等差比數列，所以
，
，所以
， 或
，最小正值等于
，此時
，（3）充分性就是驗證，易證，關鍵在于證必要性，可從兩者中在交集（共同元素）出發. 
,
成等差數列, 因此
既是
中的項，也是中的項，
既是
中的項，也是中的項，可得它們公差的關系，進而推出三者結構統一，得出等差數列的結論.
（1）
（2分） （4分）
（2）是級等差數列，（
） （1分）
（）
所以， 或對
恒成立時， 
時，
（3分）最小正值等于，此時
由于
（）
（） （5分）
（） （6分）
（3）若為級等差數列，
，則均成等差數列，（1分）
設等差數列的公差分別為
為級等差數列，，則成等差數列，設公差為
既是中的項，也是中的項，
名牌中學課時作業系列答案
明天教育課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案
周周清檢測系列答案科目：高中數學 來源： 題型：解答題
已知數列{an}中，a1＝1，an＋1＝
(n∈N*)．
(1)求證： 數列 ｛
＋
｝是等比數列，并求數列{an}的通項an
(2)若數列{bn}滿足bn＝(3n－1)
an，數列{bn}的前n項和為Tn，若不等式(－1)nλ＜Tn對一切n∈N*恒成立，求λ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
設C1、C2、…、Cn、…是坐標平面上的一列圓，它們的圓心都在軸的正半軸上，且都與直線y＝
x相切，對每一個正整數n，圓Cn都與圓Cn＋1相互外切，以rn表示Cn的半徑，已知{rn}為遞增數列．
(1)證明：{rn}為等比數列；
(2)設r1＝1，求數列
的前n項和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
首項為
，公比為q,求（1）該數列的前n項和
。
不是等比數列
的前
項和
和通項
滿足
。
滿足
，求證：
中，
，公比
，
為
，求數列
的通項公式．
，等比數列
的前n項和為
，數列
的前n項為
，且前n項和
．
的通項公式：
前n項和為
，問使
的最小正整數n是多少？
數列
滿足：
．
是等比數列（要指出首項與公比）；
的通項公式．
滿足：
，則
；