【題目】已知拋物線
：
（
），焦點為
，直線
交拋物線于
，
兩點，
為
的中點，且
．
（1）求拋物線的方程；
（2）若
，求
的最小值．
【答案】（1）
；（2）
.
【解析】試題分析：（1）（1）根據拋物線的定義知
，
，
∵
，從而可求出
，進而可得結果；（2）設直線
的方程為
，代入拋物線方程，得
，根據韋達定理，弦長公式將
用
表示，換元后利用基本不等式可得結果.
試題解析：（1）根據拋物線的定義知，，
∵，
∴，
∴．
（2）設直線的方程為，代入拋物線方程，得，
∵
，即
，
∴
，即
，
∴
，
∴
，，
，
，
∴
，
令
，
，則
．
【方法點晴】本題主要考查待定系數法求拋物線方程及圓錐曲線求最值，屬于難題.解決圓錐曲線中的最值問題一般有兩種方法：一是幾何意義，特別是用圓錐曲線的定義和平面幾何的有關結論來解決，非常巧妙；二是將圓錐曲線中最值問題轉化為函數問題，然后根據函數的特征選用參數法、配方法、判別式法、三角函數有界法、函數單調性法以及均值不等式法，本題（2）就是用的這種思路，利用均值不等式法求解的.
小學課時特訓系列答案科目：高中數學 來源： 題型：
【題目】【選修4－4：坐標系與參數方程】
已知直線l：ρsin（θ＋
）＝
m，曲線C：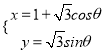 
（1）當m＝3時，判斷直線l與曲線C的位置關系；
（2）若曲線C上存在到直線l的距離等于
的點，求實數m的范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】判斷下列命題是全稱命題還是特稱命題，并判斷其真假；寫出這些命題的否定并判斷真假.
（1）三角形的內角和為180°；
（2）每個二次函數的圖象都開口向下；
（3）存在一個四邊形不是平行四邊形；
（4）
;
（5）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設全集為實數集R，函數f（x）=lg（2x﹣1）的定義域為A，集合B={x||x|﹣a≤0}（a∈R）
（1）若a=2，求A∪B和A∩B
（2）若RA∪B=RA，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方體ABCD﹣A′B′C′D′中，E是棱BC的中點，G是棱DD′的中點，則異面直線GB與B′E所成的角為（ ）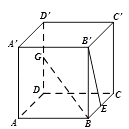 
A.120°
B.90°
C.60°
D.30°
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=a（ 
）x+bx2+cx（α∈R，b≠0，c∈R），若{x|f（x）=0}={x|f（f（x））=0}≠，則實數c的取值范圍為（ ）
A.（0，4）
B.[0，4]
C.（0，4]
D.[0，4）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，拋物線
的方程為
．
（1）以坐標原點為極點， 
軸正半軸為極軸建立極坐標系，求
的極坐標方程；
（2）直線
的參數方程是
（
為參數），
與
交于
兩點， 
，求
的斜率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
