
【題目】函數![]() ,
, ![]() .(1)討論
.(1)討論![]() 的極值點的個數;(2)若對于
的極值點的個數;(2)若對于![]() ,總有
,總有![]() .(i)求實數
.(i)求實數![]() 的取值范圍;(ii)求證:對于
的取值范圍;(ii)求證:對于![]() ,不等式
,不等式![]() 成立.
成立.
【答案】(1)當![]() 時,函數
時,函數![]() 有兩個極值點;當
有兩個極值點;當![]() 時,函數
時,函數![]() 沒有極值點. (2)①
沒有極值點. (2)①![]() ②見解析
②見解析
【解析】試題分析:(1)先求函數導數,轉化為研究二次函數![]() 實根分布:當
實根分布:當![]() ,導函數不變號,無極值;當
,導函數不變號,無極值;當![]() ,分
,分![]() 時,兩個正根,有兩個極值點;
時,兩個正根,有兩個極值點; ![]() 時,兩個負根,無極值點(2)①不等式恒成立問題利用變量分離轉化為對應函數最值問題:
時,兩個負根,無極值點(2)①不等式恒成立問題利用變量分離轉化為對應函數最值問題: 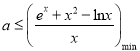 ,再利用導數研究函數
,再利用導數研究函數![]() 單調性,并得最小值
單調性,并得最小值![]() ,即得實數
,即得實數![]() 的取值范圍;②由①轉化證明
的取值范圍;②由①轉化證明![]() ,利用導數研究函數
,利用導數研究函數![]() 單調性,可得
單調性,可得![]()
試題解析: 解:由題意得![]()
![]() ,令
,令![]() ,
,
(1)當![]() ,即
,即![]() 時,
時, ![]() 對
對![]() 恒成立,
恒成立,
即![]() 對
對![]() 恒成立,此時
恒成立,此時![]() 沒有極值點;
沒有極值點;
(2)當![]() ,即
,即![]() 或
或![]() ,
,
①![]() 時,設方程
時,設方程![]() 兩個不同實根為
兩個不同實根為![]() ,不妨設
,不妨設![]() ,
,
則![]() ,
, ![]() ,故
,故![]() ,
,
![]()
![]() 或
或![]() 時,
時, ![]() ;在
;在![]() 時
時![]() ,
,
故![]() 是函數
是函數![]() 的兩個極值點.
的兩個極值點.
②![]() 時,設方程
時,設方程![]() 兩個不同實根為
兩個不同實根為![]() ,
,
則![]() ,
, ![]() ,故
,故![]() ,
, ![]() ,
,
![]()
![]() 時,
時, ![]() ;故函數
;故函數![]() 沒有極值點.
沒有極值點.
綜上,當![]() 時,函數
時,函數![]() 有兩個極值點;
有兩個極值點;
當![]() 時,函數
時,函數![]() 沒有極值點.
沒有極值點.
(2)①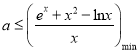 ,
, ![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,所以
單調遞增,所以![]()
②![]() 只需證明
只需證明![]() 易得
易得![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,
單調遞增, ![]() ,得證.
,得證.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x-3)ex+ax,aR
(1)當a=1時,求曲線f(x)在點(2,f(2))處的切線方程;
(2)當a[0,e)時,設函數f(x)在(1,+)上的最小值為g(a),求函數g(a)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學校本課程開設了A,B,C,D共4門選修課,每個學生必須且只能選修1門選修課,現有該校的甲、乙、丙3名學生.
(1)求這3名學生選修課所有選法的總數;
(2)求恰有2門選修課沒有被這3名學生選擇的概率;
(3)求A選修課被這3名學生選擇的人數ξ的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“中國式過馬路”是網友對部分中國人集體闖紅燈現象的一種調侃,即“湊夠一撮人就可以走了,和紅綠燈無關.”出現這種現象是大家受法不責眾的“從眾”心理影響,從而不顧及交通安全.某校對全校學生過馬路方式進行調查,在所有參與調查的人中,“跟從別人闖紅燈”“從不闖紅燈”“帶頭闖紅燈”人數如表所示:
跟從別人闖紅燈 | 從不闖紅燈 | 帶頭闖紅燈 | |
男生 | 800 | 450 | 200 |
女生 | 100 | 150 | 300 |
(1)在所有參與調查的人中,用分層抽樣的方法抽取n人,已知“跟從別人闖紅燈”的人中抽取45人,求n的值;
(2)在“帶頭闖紅燈”的人中,將男生的200人編號為1,2,…,200;將女生的300人編號為201,202,…,500,用系統抽樣的方法抽取4人參加“文明交通”宣傳活動,若抽取的第一個人的編號為100,把抽取的4人看成一個總體,從這4人中任選取2人,求這兩人均是女生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個袋子中裝有三個編號分別為1,2,3的紅球和三個編號分別為1,2,3的白球,三個紅球按其編號分別記為a1 , a2 , a3 , 三個白球按其編號分別記為b1 , b2 , b3 , 袋中的6個球除顏色和編號外沒有任何差異,現從袋中一次隨機地取出兩個球,
(1)列舉所有的基本事件,并寫出其個數;
(2)規定取出的紅球按其編號記分,取出的白球按其編號的2倍記分,取出的兩個球的記分之和為一次取球的得分,求一次取球的得分不小于6的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sinx﹣cosx+x+1,x∈[0,2π]
(1)求函數f(x)的單調遞減區間;
(2)求函數f(x)的極小值和最大值,并寫明取到極小值和最大值時分別對應x的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3﹣3x
(1)討論f(x)的單調區間;
(2)若函數g(x)=f(x)﹣m在[﹣ ![]() ,3]上有三個零點,求實數m的取值范圍;
,3]上有三個零點,求實數m的取值范圍;
(3)設函數h(x)=ex﹣ex+4n2﹣2n(e為自然對數的底數),如果對任意的x1 , x2∈[ ![]() ,2],都有f(x1)≤h(x2)恒成立,求實數n的取值范圍.
,2],都有f(x1)≤h(x2)恒成立,求實數n的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某印刷廠為了研究印刷單冊書籍的成本y(單位:元)與印刷冊數x(單位:千冊)之間的關系,在印制某種書籍時進行了統計,相關數據見下表:

根據以上數據,技術人員分別借助甲、乙兩種不同的回歸模型,得到了兩個回歸方程,甲: ![]()
為了評價兩種模型的擬合效果,完成以下任務:
(1)(ⅰ)完成下表(計算結果精確到0.1):
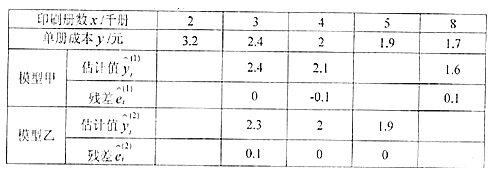
(ⅱ)分別計算模型甲與模型乙的殘差平方和![]() 及
及![]() ,并通過比較
,并通過比較![]() ,
,![]() 的大小,判斷哪個模型擬合效果更好.
的大小,判斷哪個模型擬合效果更好.
(2)該書上市后,受到廣大讀者的熱烈歡迎,不久便全部售罄,于是印刷廠決定進行二次印刷,根據市場調查,新需求量為8千冊(概率為0.8)或10千冊(概率為0.2),若印刷廠以沒測5元的價格將書籍出售給訂貨商,問印刷廠二次印刷8千冊還是10千冊恒獲得更多的利潤?(按(1)中擬合效果較好的模型計算印刷單冊書的成本)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com