
【題目】在平面直角坐標系xOy中,已知△ABC的兩個頂點A,B的坐標分別為(﹣1,0),(1,0),且AC、BC所在直線的斜率之積等于﹣2,記頂點C的軌跡為曲線E.
(1)求曲線E的方程;
(2)設(shè)直線y=2x+m(m∈R且m≠0)與曲線E相交于P、Q兩點,點M( ![]() ,1),求△MPQ面積的取值范圍.
,1),求△MPQ面積的取值范圍.
【答案】
(1)解:設(shè)C(x,y),由題意,可得 ![]() =﹣2(x≠±1),
=﹣2(x≠±1),
∴曲線E的方程為 ![]() =1(x≠±1)
=1(x≠±1)
(2)解:設(shè)P(x1,y1),Q(x2,y2),
聯(lián)立 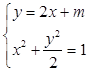 ,消去y,得6x2+4mx+m2﹣2=0,
,消去y,得6x2+4mx+m2﹣2=0,
∵△=48﹣8m2>0,∴m2<6,
∵x≠±1,∴m≠±2,
又∵m≠0,∴0<m2<6,且m2≠4,
∵ ![]() ,
, ![]() ,
,
∴|PQ|= ![]() |x1﹣x2|=
|x1﹣x2|= ![]()
![]()
= ![]()
= ![]()
![]() .
.
點M( ![]() ,1)到PQ的距離d=
,1)到PQ的距離d= ![]() =
= ![]() ,
,
∵0<m2<6,m2≠4,
∴ ![]() =(
=( ![]() )2=
)2= ![]() =
= ![]() m2m2(12﹣2m2)
m2m2(12﹣2m2)
≤ ![]() (
( ![]() )3=
)3= ![]() =
= ![]() ,
,
當且僅當m2=12﹣2m2時,取等號,又m2≠4,
∴ ![]() ∈(0,
∈(0, ![]() ).
).
∴△MPQ面積的取值范圍是(0, ![]() )
)
【解析】(1)設(shè)C(x,y),由題意,可得 ![]() =﹣2(x≠±1),由此能求出曲線E的方程.(2)設(shè)P(x1,y1),Q(x2,y2),聯(lián)立
=﹣2(x≠±1),由此能求出曲線E的方程.(2)設(shè)P(x1,y1),Q(x2,y2),聯(lián)立  ,得6x2+4mx+m2﹣2=0,由此利用根的判別式、韋達定理、弦長公式、三角形面積公式,結(jié)合已知條件能求出△MPQ面積的取值范圍.
,得6x2+4mx+m2﹣2=0,由此利用根的判別式、韋達定理、弦長公式、三角形面積公式,結(jié)合已知條件能求出△MPQ面積的取值范圍.


 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}滿足a1=1,Sn=2an+1 , 其中Sn為{an}的前n項和(n∈N*).
(Ⅰ)求S1 , S2及數(shù)列{Sn}的通項公式;
(Ⅱ)若數(shù)列{bn}滿足 ![]() ,且{bn}的前n項和為Tn , 求證:當n≥2時,
,且{bn}的前n項和為Tn , 求證:當n≥2時, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知中心在原點,焦點在x軸上的橢圓的一個焦點為( ![]() ,0),(1,
,0),(1, ![]() )是橢圓上的一個點.
)是橢圓上的一個點. 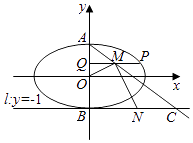
(1)求橢圓的標準方程;
(2)設(shè)橢圓的上、下頂點分別為A,B,P(x0 , y0)(x0≠0)是橢圓上異于A,B的任意一點,PQ⊥y軸,Q為垂足,M為線段PQ中點,直線AM交直線l:y=﹣1于點C,N為線段BC的中點,如果△MON的面積為 ![]() ,求y0的值.
,求y0的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義在(﹣1,+∞)上的單調(diào)函數(shù)f(x),對于任意的x∈(﹣1,+∞),f[f(x)﹣xex]=0恒成立,則方程f(x)﹣f′(x)=x的解所在的區(qū)間是( )
A.(﹣1,﹣ ![]() )
)
B.(0, ![]() )
)
C.(﹣ ![]() ,0)
,0)
D.( ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=|2x+ ![]() |+a|x﹣
|+a|x﹣ ![]() |.
|.
(Ⅰ)當a=﹣1時,解不等式f(x)≤3x;
(Ⅱ)當a=2時,若關(guān)于x的不等式2f(x)+1<|1﹣b|的解集為空集,求實數(shù)b的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若f(x)=sin(2x+φ)+b,對任意實數(shù)x都有f(x+ ![]() )=f(﹣x),f(
)=f(﹣x),f( ![]() )=﹣1,則實數(shù)b的值為( )
)=﹣1,則實數(shù)b的值為( )
A.﹣2或0
B.0或1
C.±1
D.±2
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓 ![]() 的右焦點
的右焦點 ![]() ,且經(jīng)過點
,且經(jīng)過點 ![]() ,點M是x軸上的一點,過點M的直線l與橢圓C交于A,B兩點(點A在x軸的上方)
,點M是x軸上的一點,過點M的直線l與橢圓C交于A,B兩點(點A在x軸的上方) 
(1)求橢圓C的方程;
(2)若|AM|=2|MB|,且直線l與圓 ![]() 相切于點N,求|MN|的長.
相切于點N,求|MN|的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)f(x)=|x﹣1|+|x+1|,(x∈R)
(1)求證:f(x)≥2;
(2)若不等式f(x)≥ ![]() 對任意非零實數(shù)b恒成立,求x的取值范圍.
對任意非零實數(shù)b恒成立,求x的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com