
【題目】設橢圓C: ![]() 的一個頂點與拋物線
的一個頂點與拋物線![]() 的焦點重合,
的焦點重合, ![]() 分別是橢圓的左、右焦點,且離心率
分別是橢圓的左、右焦點,且離心率![]() ,過橢圓右焦點
,過橢圓右焦點![]() 的直線l與橢圓C交于
的直線l與橢圓C交于![]() 兩點.
兩點.
(1)求橢圓C的方程;
(2)若![]() ,求直線l的方程;
,求直線l的方程;
(3)若![]() 是橢圓C經過原點O的弦,
是橢圓C經過原點O的弦, ![]() ,求證:
,求證: ![]() 為定值.
為定值.
【答案】(1) ![]() ;(2) y=
;(2) y=![]() (x-1)或y=-
(x-1)或y=-![]() (x-1);(3)見解析.
(x-1);(3)見解析.
【解析】試題分析:(1)由題意,橢圓的標準方程為![]() +
+![]() =1;(2)設直線l的方程為y=k(x-1)(k≠0),
=1;(2)設直線l的方程為y=k(x-1)(k≠0),![]() ·
·![]() =x1x2+y1y2=-2,利用韋達定理,解得答案;(3)|MN|=
=x1x2+y1y2=-2,利用韋達定理,解得答案;(3)|MN|=![]() |x1-x2|,|AB|=
|x1-x2|,|AB|=![]() |x3-x4|,代入韋達定理計算,得到答案。
|x3-x4|,代入韋達定理計算,得到答案。
試題解析:
(1)橢圓的頂點為(0,![]() ),即b=
),即b=![]() ,e=
,e=![]() =
=![]() ,∴a=2,∴橢圓的標準方程為
,∴a=2,∴橢圓的標準方程為![]() +
+![]() =1.
=1.
(2)由題可知,直線l與橢圓必相交.
①當直線斜率不存在時,經檢驗不合題意.
②當斜率存在時,設直線l的方程為y=k(x-1)(k≠0),
且M(x1,y1),N(x2,y2).
由 得(3+4k2)x2-8k2x+4k2-12=0,x1+x2=
得(3+4k2)x2-8k2x+4k2-12=0,x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
![]() ·
·![]() =x1x2+y1y2=x1x2+k2[x1x2-(x1+x2)+1]
=x1x2+y1y2=x1x2+k2[x1x2-(x1+x2)+1]
=![]() +k2
+k2![]()
=![]() =-2,解得k=±
=-2,解得k=±![]() ,
,
故直線l的方程為y=![]() (x-1)或y=-
(x-1)或y=-![]() (x-1).
(x-1).
(3)證明:設M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4),
由(2)可得|MN|=![]() |x1-x2|
|x1-x2|
=![]()
=![]()
=![]() ,
,
由 消去y并整理得x2=
消去y并整理得x2=![]() ,
,
|AB|=![]() |x3-x4|=4
|x3-x4|=4![]() ,
,
∴![]() =
= =4,為定值.
=4,為定值.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知:三棱錐![]() 中,側面
中,側面![]() 垂直底面,
垂直底面, ![]() 是底面最長的邊;圖1是三棱錐
是底面最長的邊;圖1是三棱錐![]() 的三視圖,其中的側視圖和俯視圖均為直角三角形;圖2是用斜二測畫法畫出的三棱錐
的三視圖,其中的側視圖和俯視圖均為直角三角形;圖2是用斜二測畫法畫出的三棱錐![]() 的直觀圖的一部分,其中點
的直觀圖的一部分,其中點![]() 在
在![]() 平面內.
平面內.
(Ⅰ)請在圖2中將三棱錐![]() 的直觀圖補充完整,并指出三棱錐
的直觀圖補充完整,并指出三棱錐![]() 的哪些面是直角三角形;
的哪些面是直角三角形;![]()
![]()
(Ⅱ)設二面角![]() 的大小為
的大小為![]() ,求
,求![]() 的值;
的值;
(Ⅲ)求點![]() 到面
到面![]() 的距離.
的距離.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)在R上可導,其導函數為f′(x),且函數y=(1-x)f′(x)的圖像如圖所示,則下列結論中一定成立的是( )
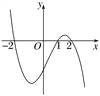
A. 函數f(x)有極大值f(2)和極小值f(1) B. 函數f(x)有極大值f(-2)和極小值f(1)
C. 函數f(x)有極大值f(2)和極小值f(-2) D. 函數f(x)有極大值f(-2)和極小值f(2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
: ![]() 的焦點為
的焦點為![]() ,準線為
,準線為![]() ,三個點
,三個點![]() ,
, ![]() ,
, ![]() 中恰有兩個點在
中恰有兩個點在![]() 上.
上.
(1)求拋物線![]() 的標準方程;
的標準方程;
(2)過![]() 的直線交
的直線交![]() 于
于![]() ,
, ![]() 兩點,點
兩點,點![]() 為
為![]() 上任意一點,證明:直線
上任意一點,證明:直線![]() ,
, ![]() ,
, ![]() 的斜率成等差數列.
的斜率成等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某大型景區有兩條直線型觀光路線![]() ,
, ![]() ,
,![]() ,點
,點![]() 位于
位于![]() 的平分線上,且與頂點
的平分線上,且與頂點![]() 相距1公里.現準備過點
相距1公里.現準備過點![]() 安裝一直線型隔離網
安裝一直線型隔離網![]() (
(![]() 分別在
分別在![]() 和
和![]() 上),圍出三角形區域
上),圍出三角形區域![]() ,且
,且![]() 和
和![]() 都不超過5公里.設
都不超過5公里.設![]() ,
, ![]() (單位:公里).
(單位:公里).
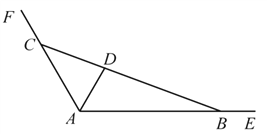
(Ⅰ)求![]() 的關系式;
的關系式;
(Ⅱ)景區需要對兩個三角形區域![]() ,
, ![]() 進行綠化.經測算,
進行綠化.經測算, ![]() 區城每平方公里的綠化費用是
區城每平方公里的綠化費用是![]() 區域的兩倍,試確定
區域的兩倍,試確定![]() 的值,使得所需的總費用最少.
的值,使得所需的總費用最少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】4月23日是“世界讀書日”,某中學在此期間開展了一系列的讀書教育活動,為了解本校學生課外閱讀情況,學校隨機抽取了100名學生對其課外閱讀時間進行調查,下面是根據調查結果繪制的學生日均課外閱讀時間(單位:min)的頻率分布直方圖,若將日均課外閱讀時間不低于60 min的學生稱為“書蟲”,低于60 min的學生稱為“懶蟲”,

(1)求x的值并估計全校3 000名學生中“書蟲”大概有多少名學生?(將頻率視為概率)
(2)根據已知條件完成下面2×2的列聯表,并判斷能否在犯錯誤的概率不超過0.01的前提下認為“書蟲”與性別有關:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為研究患肺癌與是否吸煙有關,某腫瘤機構隨機抽取了40人做相關調查,其中不吸煙人數與吸煙人數相同,已知吸煙人數中,患肺癌與不患肺癌的比為![]() ;不吸煙的人數中,患肺癌與不患肺癌的比為
;不吸煙的人數中,患肺癌與不患肺癌的比為![]() .
.
(1)現從患肺癌的人中用分層抽樣的方法抽取5人,再從這5人中隨機抽取2人進行調查,求這兩人都是吸煙患肺癌的概率;
(2)是否有99.9%的把握認為患肺癌與吸煙有關?
附: 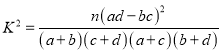 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點的雙曲線![]() 的右焦點為
的右焦點為![]() ,右頂點為
,右頂點為![]() ,(
,( ![]() 為原點)
為原點)
(1)求雙曲線![]() 的方程;
的方程;
(2)若直線![]() :
: ![]() 與雙曲線恒有兩個不同的交點
與雙曲線恒有兩個不同的交點![]() 和
和![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 關于
關于![]() 軸對稱,頂點在坐標原點
軸對稱,頂點在坐標原點![]() ,直線
,直線![]() 經過拋物線
經過拋物線![]() 的焦點.
的焦點.
(1)求拋物線![]() 的標準方程;
的標準方程;
(2)若不經過坐標原點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 相交于不同的兩點
相交于不同的兩點![]() ,
, ![]() ,且滿足
,且滿足![]() ,證明直線
,證明直線![]() 過
過![]() 軸上一定點
軸上一定點![]() ,并求出點
,并求出點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com