
【題目】設定義在![]() 上的函數
上的函數![]() 滿足任意
滿足任意![]() 都有
都有![]() ,且
,且![]() 時,
時,![]() ,則
,則![]() ,
,![]() ,
,![]() 的大小關系是( )
的大小關系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
函數f(x)滿足f(t+2)=![]() ,可得f(x)是周期為4的函數.6f(2017)=6f(1),3f(2018)
,可得f(x)是周期為4的函數.6f(2017)=6f(1),3f(2018)
=3f(2),2f(2019)=2f(3).令g(x)=![]() ,x∈(0,4],則g′(x)=
,x∈(0,4],則g′(x)=![]() >0,利
>0,利
用其單調性即可得出.
函數f(x)滿足f(t+2)=![]() ,可得f(t+4)=
,可得f(t+4)=![]() =f(t),∴f(x)是周期為4的函數.
=f(t),∴f(x)是周期為4的函數.
6f(2017)=6f(1),3f(2018)=3f(2),2f(2019)=2f(3).
令g(x)=![]() ,x∈(0,4],則g′(x)=
,x∈(0,4],則g′(x)=![]() ,
,
∵x∈(0,4]時,![]() ,
,
∴g′(x)>0,g(x)在(0,4]遞增,
∴f(1)<![]() <
<![]() ,
,
可得:6f(1)<3f(2)<2f(3),即6f(2017)<3f(2018)<2f(2019).
故答案為:A


 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案 名校名卷單元同步訓練測試題系列答案
名校名卷單元同步訓練測試題系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)![]() 為曲線
為曲線![]() 上的動點,點
上的動點,點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() ,求點
,求點![]() 的軌跡
的軌跡![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的極坐標為
的極坐標為![]() ,點
,點![]() 在曲線
在曲線![]() 上,求
上,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)當a>0時,求函數f(x)的單調區間;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,過點
中,過點![]() 的直線
的直線![]() 的參數方程為
的參數方程為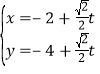 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,已知曲線
軸正半軸為極軸,建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,記直線
,記直線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() 兩點.
兩點.
(1)求曲線![]() 和
和![]() 的直角坐標方程;
的直角坐標方程;
(2)證明:![]() 成等比數列.
成等比數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在全國第五個“扶貧日”到來之前,某省開展“精準扶貧,攜手同行”的主題活動,某貧困縣調查基層干部走訪貧困戶數量.![]() 鎮有基層干部60人,
鎮有基層干部60人,![]() 鎮有基層干部60人,
鎮有基層干部60人,![]() 鎮有基層干部80人,每人都走訪了若干貧困戶,按照分層抽樣,從
鎮有基層干部80人,每人都走訪了若干貧困戶,按照分層抽樣,從![]() 三鎮共選40名基層干部,統計他們走訪貧困戶的數量,并將走訪數量分成5組,
三鎮共選40名基層干部,統計他們走訪貧困戶的數量,并將走訪數量分成5組,![]() ,繪制成如圖所示的頻率分布直方圖.
,繪制成如圖所示的頻率分布直方圖.
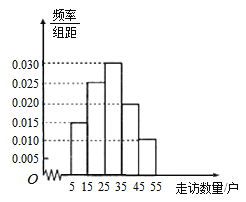
(1)求這40人中有多少人來自![]() 鎮,并估計
鎮,并估計![]() 三鎮的基層干部平均每人走訪多少貧困戶;(同一組中的數據用該組區間的中點值作代表)
三鎮的基層干部平均每人走訪多少貧困戶;(同一組中的數據用該組區間的中點值作代表)
(2)如果把走訪貧困戶達到或超過25戶視為工作出色,以頻率估計概率,從![]() 三鎮的所有基層干部中隨機選取3人,記這3人中工作出色的人數為
三鎮的所有基層干部中隨機選取3人,記這3人中工作出色的人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 過定點
過定點![]() 且在
且在![]() 軸上截得的弦長為4。
軸上截得的弦長為4。
(1)求動圓![]() 的圓心
的圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 的動直線與曲線
的動直線與曲線![]() 交于
交于![]() 兩點,點
兩點,點![]() 在曲線
在曲線![]() 上,使得
上,使得![]() 的重心
的重心![]() 在
在![]() 軸上,直線
軸上,直線![]() 交
交![]() 軸于點
軸于點![]() ,且點
,且點![]() 在點
在點![]() 的右側,記
的右側,記![]() 的面積為
的面積為![]() 的面積為
的面積為![]() ,求
,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市自2014年至2019年每年年初統計得到的人口數量如表所示.
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人數(單位:萬) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)設第![]() 年的人口數量為
年的人口數量為![]() (2014年為第1年),根據表中的數據,描述該城市人口數量和2014年至2018年每年該城市人口的增長數量的變化趨勢;
(2014年為第1年),根據表中的數據,描述該城市人口數量和2014年至2018年每年該城市人口的增長數量的變化趨勢;
(2)研究統計人員用函數![]() 擬合該城市的人口數量,其中
擬合該城市的人口數量,其中![]() 的單位是年.假設2014年初對應
的單位是年.假設2014年初對應![]() ,
,![]() 的單位是萬.設
的單位是萬.設![]() 的反函數為
的反函數為![]() ,求
,求![]() 的值(精確到0.1),并解釋其實際意義.
的值(精確到0.1),并解釋其實際意義.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某生鮮批發店每天從蔬菜生產基地以5元/千克購進某種綠色蔬菜,售價8元/千克,若每天下午4點以前所購進的綠色蔬菜沒有售完,則對未售出的綠色蔬菜降價處理,以3元/千克出售.根據經驗,降價后能夠把剩余蔬菜全部處理完畢,且當天不再進貨.該生鮮批發店整理了過往30天(每天下午4點以前)這種綠色蔬菜的日銷售量(單位:千克)得到如下統計數據(視頻率為概率)(注:x,y∈N*)
每天下午4點前銷售量 | 350 | 400 | 450 | 500 | 550 |
天數 | 3 | 9 | x | y | 2 |
(1)求在未來3天中,至少有1天下午4點前的銷售量不少于450千克的概率.
(2)若該生鮮批發店以當天利潤期望值為決策依據,當購進450千克比購進500千克的利潤期望值大時,求x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com