
【題目】在直角坐標系xOy中,直線l的參數(shù)方程為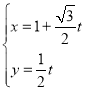 (t為參數(shù)),在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為ρsin2θ=4cosθ.
(t為參數(shù)),在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C的極坐標方程為ρsin2θ=4cosθ.
(1)求直線l的普通方程與曲線C的直角坐標方程;
(2)若直線l與x軸的交點為F,直線l與曲線C的交點為A、B,求|FA|+|FB|的值.
【答案】(1)直線l的普通方程為![]() ,曲線C的直角坐標方程為y2=4x
,曲線C的直角坐標方程為y2=4x
(2)16
【解析】
(1)消參即可求出直線l的普通方程,由![]() 代入即可求出曲線C的直角坐標方程.
代入即可求出曲線C的直角坐標方程.
(2)將直線的參數(shù)方程代入曲線方程,根據(jù)韋達定理求出![]() ,t1t2=﹣16(t1和t2為A、B對應(yīng)的參數(shù)),由
,t1t2=﹣16(t1和t2為A、B對應(yīng)的參數(shù)),由![]() 即可求解.
即可求解.
(1)直線l的參數(shù)方程為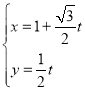 (t為參數(shù)),轉(zhuǎn)換為直角坐標方程為
(t為參數(shù)),轉(zhuǎn)換為直角坐標方程為![]() .
.
曲線C的極坐標方程為ρsin2θ=4cosθ.整理得(ρsinθ)2=4ρcosθ,轉(zhuǎn)換為直角坐標方程為y2=4x.
(2)由于直線l與x軸的交點坐標為(1,0),所以把直線l的參數(shù)方程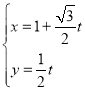 (t為參數(shù))代入y2=4x,
(t為參數(shù))代入y2=4x,
得到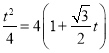 ,即
,即![]() ,
,
所以![]() ,t1t2=﹣16(t1和t2為A、B對應(yīng)的參數(shù)),
,t1t2=﹣16(t1和t2為A、B對應(yīng)的參數(shù)),
所以|FA|+|FB|![]() .
.


 期末沖刺100分創(chuàng)新金卷完全試卷系列答案
期末沖刺100分創(chuàng)新金卷完全試卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
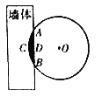
【題目】《九章算術(shù)》是我國古代數(shù)學(xué)經(jīng)典名著,其中有這樣一個問題:“今有圓材,埋在壁中,不知大小.以鋸鋸之,深一寸,鋸道長一尺.問徑幾何?”其意為:今有-圓柱形木材,埋在墻壁中,不知其大小,用鋸去鋸該木材,鋸口深一寸,鋸道長-尺.問這塊圓柱形木材的直徑是多少?現(xiàn)有長為1丈的圓柱形木材部分鑲嵌在墻體中,截面圖如圖所示(陰影部分為鑲嵌在墻體內(nèi)的部分).已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算該木材鑲嵌在墻體中的體積約為__________立方寸.(結(jié)果保留整數(shù))
寸,估算該木材鑲嵌在墻體中的體積約為__________立方寸.(結(jié)果保留整數(shù))
注:l丈=10尺=100寸,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某調(diào)查機構(gòu)為了解人們對某個產(chǎn)品的使用情況是否與性別有關(guān),在網(wǎng)上進行了問卷調(diào)查,在調(diào)查結(jié)果中隨機抽取了![]() 份進行統(tǒng)計,得到如下
份進行統(tǒng)計,得到如下![]() 列聯(lián)表:
列聯(lián)表:
男性 | 女性 | 合計 | |
使用 | 15 | 5 | 20 |
不使用 | 10 | 20 | 30 |
合計 | 25 | 25 | 50 |
(1)請根據(jù)調(diào)查結(jié)果你有多大把握認為使用該產(chǎn)品與性別有關(guān);
(2)在不使用該產(chǎn)品的人中,按性別用分層抽樣抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人參加某項活動,記被抽中參加該項活動的女性人數(shù)為
人參加某項活動,記被抽中參加該項活動的女性人數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
附: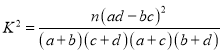 ,
,
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)設(shè)![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線在
處的切線在![]() 軸上的截距為
軸上的截距為![]() ,求
,求![]() 的最小值;
的最小值;
(Ⅱ)若![]() 只有一個零點,求實數(shù)
只有一個零點,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線C的極坐標方程是![]() ,以極點為原點,極軸為x軸的正半軸建立平面直角坐標系,曲線C經(jīng)過伸縮變換
,以極點為原點,極軸為x軸的正半軸建立平面直角坐標系,曲線C經(jīng)過伸縮變換 得到曲線E,直線l:
得到曲線E,直線l: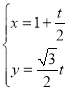 (t為參數(shù))與曲線E交于A,B兩點,
(t為參數(shù))與曲線E交于A,B兩點,
(1)設(shè)曲線C上任一點為![]() ,求
,求![]() 的最小值;
的最小值;
(2)求出曲線E的直角坐標方程,并求出直線l被曲線E截得的弦AB長;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(2017·江蘇高考)如圖,在三棱錐ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,點E,F(E與A,D不重合)分別在棱AD,BD上,且EF⊥AD.

求證:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
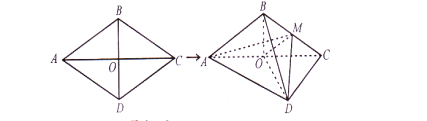
【題目】如圖,菱形![]() 的邊長為
的邊長為![]() ,
,![]() ,
,![]() 與
與![]() 交于
交于![]() 點.將菱形
點.將菱形![]() 沿對角線
沿對角線![]() 折起,得到三棱錐
折起,得到三棱錐![]() ,點
,點![]() 是棱
是棱![]() 的中點,
的中點,![]() .
.
(I)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(II)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】試比較下面概率的大小:
(1)如果以連續(xù)擲兩次骰子依次得到的點數(shù)m,n作為點P的橫、縱坐標,點P在直線![]() 的下面
的下面![]() 包括直線
包括直線![]() 的概率
的概率![]() ;
;
(2)在正方形![]() ,
,![]() ,x,
,x,![]() ,隨機地投擲點P,求點P落在正方形T內(nèi)直線
,隨機地投擲點P,求點P落在正方形T內(nèi)直線![]() 的下面
的下面![]() 包括直線
包括直線![]() 的概率
的概率![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,
,![]() 是橢圓
是橢圓![]() 上一點,
上一點,![]() 軸,
軸,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,
,![]() 為坐標原點,且
為坐標原點,且![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com