
已知拋物線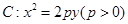 ,直線
,直線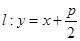 交拋物線于
交拋物線于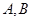 兩點,且
兩點,且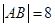 .
.
(1)求拋物線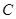 的方程;
的方程;
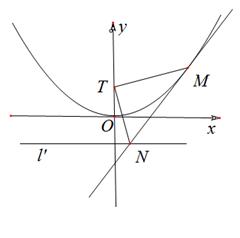
(2)若點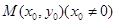 是拋物線
是拋物線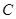 上的動點,過
上的動點,過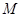 點的拋物線的切線與直線
點的拋物線的切線與直線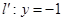 交于點
交于點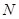 ,問在
,問在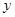 軸上是否存在定點
軸上是否存在定點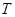 ,使得
,使得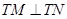 ?若存在,求出該定點,并求出
?若存在,求出該定點,并求出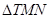 的面積的最小值;若不存在,請說明理由.
的面積的最小值;若不存在,請說明理由.
(1)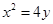 .(2)存在定點(0,1),
.(2)存在定點(0,1),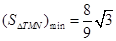 .
.
【解析】
試題分析:(1)把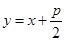 代入
代入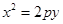 ,消去
,消去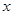 ,整理得
,整理得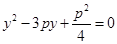 ,
,
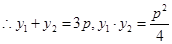 2分
2分
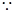
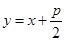 過拋物線的焦點
過拋物線的焦點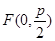 ,
,
 拋物線
拋物線 的方程為
的方程為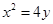 .
6分
.
6分
(2)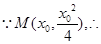 切線方程為
切線方程為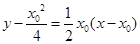 ,即
,即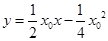 ,
,
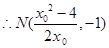 8分
8分
令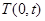 ,
,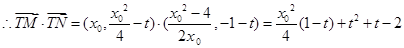 ,
,
當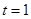 時,
時,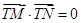 ,即
,即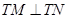 ,
,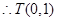 10分
10分
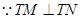 ,
,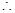
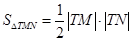 ,
,
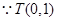 點是拋物線的焦點,
點是拋物線的焦點,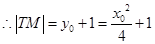 ,
,
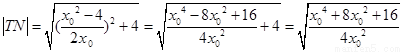
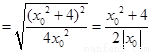 ,
,
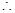
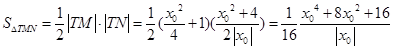 ,
13分
,
13分
不妨設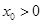 ,令
,令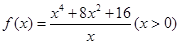 ,
,
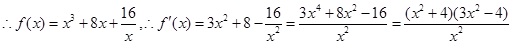 ,
,
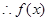 在
在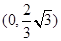 上遞減,在
上遞減,在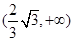 上遞增,
上遞增,
 ,
,
即當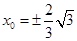 時,
時,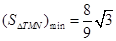 . 15分
. 15分
考點:本題考查了直線與拋物線的綜合運用
點評:解決拋物線中的定值及最值問題的基本思想是建立目標函數和建立不等式(方程)關系,根據條件求解定值及最值,因此這里問題的難點就是如何建立目標函數和不等式(或等量關系)。建立目標函數的關鍵是選用一個合適變量,這個變量可以是直線的斜率、直線的截距、點的坐標等,要根據實際情況靈活處理。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
| 2m |
| 3 |
| x2 |
| 4m2 |
| y2 |
| 3m2 |
| 2m |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分18分)第一題滿分4分,第二題滿分6分,第三題滿分8分.
已知橢圓![]() 的長軸長是焦距的兩倍,其左、右焦點依次為
的長軸長是焦距的兩倍,其左、右焦點依次為![]() 、
、![]() ,拋物線
,拋物線![]()
![]() 的準線與
的準線與![]() 軸交于
軸交于![]() ,橢圓
,橢圓![]() 與拋物線
與拋物線![]() 的一個交點為
的一個交點為![]() .
.
(1)當![]() 時,求橢圓
時,求橢圓![]() 的方程;
的方程;
(2)在(1)的條件下,直線![]() 過焦點
過焦點![]() ,與拋物線
,與拋物線![]() 交于
交于![]() 兩點,若弦長
兩點,若弦長![]() 等于
等于![]() 的周長,求直線
的周長,求直線![]() 的方程;
的方程;
(3)由拋物線弧![]()
![]() 和橢圓弧
和橢圓弧![]()
![]()
(![]() )合成的曲線叫“拋橢圓”,是否存在以原點
)合成的曲線叫“拋橢圓”,是否存在以原點![]() 為直角頂點,另兩個頂點
為直角頂點,另兩個頂點![]() 落在“拋橢圓”上的等腰直角三角形
落在“拋橢圓”上的等腰直角三角形![]() ,若存在,求出兩直角邊所在直線的斜率;若不存在,說明理由.
,若存在,求出兩直角邊所在直線的斜率;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源:2011年上海市浦東新區高考數學三模試卷(理科)(解析版) 題型:解答題
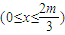 和橢圓弧
和橢圓弧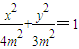

查看答案和解析>>
科目:高中數學 來源:2011年上海市浦東新區高考數學三模試卷(理科)(解析版) 題型:解答題
 和橢圓弧
和橢圓弧

查看答案和解析>>
科目:高中數學 來源: 題型:
如圖,已知拋物線方程為![]() .
.
⑴直線![]() 過拋物線的焦點F,且垂直于x軸,
過拋物線的焦點F,且垂直于x軸,![]() 與拋物線交于
與拋物線交于
A、B兩點,求AB的長度.
⑵直線![]() 過拋物線的焦點
過拋物線的焦點![]() ,且傾斜角為
,且傾斜角為![]() ,直線
,直線![]() 與拋
與拋
物線相交于C、D兩點,O為原點.求△OCD的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com