
(08年龍巖一中模擬)(12分)
如圖,三棱錐P―ABC中, PC![]() 平面ABC,PC=AC=2,AB=BC,D是PB上一點,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一點,且CD![]() 平面PAB.
平面PAB.
(Ⅰ) 求證:AB![]() 平面PCB;
平面PCB;
(Ⅱ)求異面直線AP與BC所成角的大小;
(Ⅲ)求二面角C-PA-B的大小的余弦值.

解析:解法一:
(I) ∵PC![]() 平面ABC,
平面ABC,![]()
![]() 平面ABC,∴PC
平面ABC,∴PC![]() AB.
AB.
∵CD![]() 平面PAB,
平面PAB,![]() 平面PAB,∴CD
平面PAB,∴CD![]() AB. …………………………2分
AB. …………………………2分
又![]() ,∴AB
,∴AB![]() 平面PCB. ……………………… 4分
平面PCB. ……………………… 4分
(II) 過點A作AF//BC,且AF=BC,連結PF,CF.
則![]() 為異面直線PA與BC所成的角.………5分
為異面直線PA與BC所成的角.………5分
由(Ⅰ)可得AB⊥BC,∴CF![]() AF.
AF.
由三垂線定理,得PF![]() AF.
AF.
則AF=CF=![]() ,PF=
,PF=![]() ,
,
在![]() 中, tan∠PAF=
中, tan∠PAF=![]() =
=![]() ,
,
∴異面直線PA與BC所成的角為![]() . ……………………………8分
. ……………………………8分
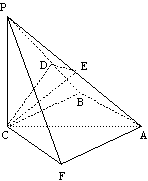
(III)取AP的中點E,連結CE、DE.
∵PC=AC=2, ∴CE ![]() PA,CE=
PA,CE=![]() .
.
∵CD![]() 平面PAB, 由三垂線定理的逆定理,得 DE
平面PAB, 由三垂線定理的逆定理,得 DE![]() PA.
PA.
∴![]() 為二面角C-PA-B的平面角. …………………………………10分
為二面角C-PA-B的平面角. …………………………………10分
由(I) AB![]() 平面PCB,又∵AB=BC,可求得BC=
平面PCB,又∵AB=BC,可求得BC=![]() .
.
在![]() 中,PB=
中,PB=![]() ,
,
![]() .
.
在![]() 中, cos
中, cos![]() =
=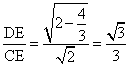 .
.
∴二面角C-PA-B大小的余弦值為![]() . …………………………12分
. …………………………12分
解法二:(I)同解法一. ………4分
(II) 由(I) AB![]() 平面PCB,∵PC=AC=2,又∵AB=BC,可求得BC=
平面PCB,∵PC=AC=2,又∵AB=BC,可求得BC=![]() .
.
以B為原點,如圖建立坐標系.
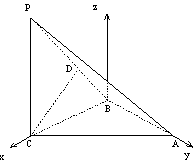
則A(0,![]() ,0),B(0,0,0),
,0),B(0,0,0),
C(![]() ,0,0),P(
,0,0),P(![]() ,0,2).
,0,2).
![]() ,
,![]() .…6分
.…6分
則![]() +0+0=2.
+0+0=2.
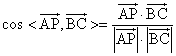 =
=![]() =
= ![]() .
.
∴異面直線AP與BC所成的角為![]() . …………………………8分
. …………………………8分
(III)設平面PAB的法向量為![]() = (x,y,z).
= (x,y,z).
![]() ,
,![]() ,
,
則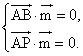 即
即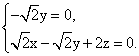
![]()
解得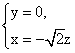 令
令![]() = -1, 得
= -1, 得![]() = (
= (![]() ,0,-1). …………………10分
,0,-1). …………………10分
設平面PAC的法向量為![]() =(
=(![]() ).
).
![]() ,
,![]() ,
,
則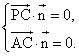 即
即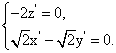
解得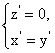 令
令![]() =1, 得
=1, 得 ![]() = (1,1,0).
= (1,1,0).
 =
=![]() .
.
∴二面角C-PA-B大小的余弦值為![]() . ……………………12分
. ……………………12分


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
(08年龍巖一中模擬文)(12分)
設a、b、c分別是先后三次拋擲一枚骰子得到的點數。
(Ⅰ)求a+b+c為奇數的概率
(Ⅱ)設有關于![]() 的一元二次方程
的一元二次方程![]() ,求上述方程有兩個不相等實根的概率.
,求上述方程有兩個不相等實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年龍巖一中模擬理)(14分)
已知函數![]() ,
,![]() .
.
(1)證明:當![]() 時,
時,![]() 在
在![]() 上是增函數;
上是增函數;
(2)對于給定的閉區間![]() ,試說明存在實數
,試說明存在實數 ![]() ,當
,當![]() 時,
時,![]() 在閉區間
在閉區間![]() 上是減函數;
上是減函數;
(3)證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年龍巖一中模擬)(12分)
盒內有大小相同的9個球,其中2個紅色球,3個白色球,4個黑色球. 規定取出1個紅色球得1分,取出1個白色球得0分,取出1個黑色球得![]() 分. 現從盒內一次性取3個球.
分. 現從盒內一次性取3個球.
(Ⅰ)求取出的3個球得分之和恰為1分的概率;
(Ⅱ)設![]() 為取出的3個球中白色球的個數,求
為取出的3個球中白色球的個數,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com