
【題目】如圖,五面體ABCDE,四邊形ABDE是矩形,△ABC是正三角形,AB=1,AE=2,F是線段BC上一點,直線BC與平面ABD所成角為30°,CE∥平面ADF.
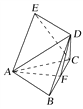
(1)試確定F的位置;
(2)求三棱錐A-CDF的體積.
【答案】(1)F是BC的中點.(2) ![]() .
.
【解析】試題分析:(1)連接BE交AD于點O,取BC的中點F,再根據三角形中位線性質得CE∥OF,最后根據線面平行判定定理得線面平行(2)根據直線BC與平面ABD所成角為30°,可得C到平面ABD的距離,再利用等體積法求三棱錐A-CDF的體積.
試題解析:(1)證明 連接BE交AD于點O,連接OF,
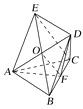
∵CE∥平面ADF,CE平面BEC,平面ADF∩平面BEC=OF,∴CE∥OF.
∵O是BE的中點,∴F是BC的中點.
(2)解 ∵BC與平面ABD所成角為30°,BC=AB=1,
∴C到平面ABD的距離為h=BC·sin 30°=![]() .
.
∵AE=2,∴VA-CDF=VF-ACD=![]() VB-ACD=
VB-ACD=![]() VC-ABD=
VC-ABD=![]() ×
×![]() ×
×![]() ×1×2×
×1×2×![]() =
=![]() .
.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】如圖,點![]() 是圓
是圓![]() 內的一個定點,點
內的一個定點,點![]() 是圓
是圓![]() 上的任意一點,線段
上的任意一點,線段![]() 的垂直平分線
的垂直平分線![]() 和半徑
和半徑![]() 相交于點
相交于點![]() ,當點
,當點![]() 在圓
在圓![]() 上運動時,點
上運動時,點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
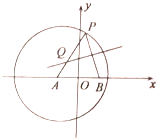
(1)求曲線![]() 的方程;
的方程;
(2)點![]() ,
, ![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設滿足以下兩個條件的有窮數列![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 階“期待數列”:
階“期待數列”:
①![]() ;
;
②![]() .
.
(![]() )分別寫出一個單調遞增的
)分別寫出一個單調遞增的![]() 階和
階和![]() 階“期待數列”.
階“期待數列”.
(![]() )若某
)若某![]() 階“期待數列”是等差數列,求該數列的通項公式.
階“期待數列”是等差數列,求該數列的通項公式.
(![]() )記
)記![]() 階“期待數列”的前
階“期待數列”的前![]() 項和為
項和為![]() ,試證:
,試證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|ax-2|.
(1)當a=2時,解不等式f(x)>x+1;
(2)若關于x的不等式f(x)+f(-x)< ![]() 有實數解,求m的取值范圍.
有實數解,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某運輸公司接受了向一地區每天至少運送180 t物資的任務,該公司有8輛載重為6 t的A型卡車和4輛載重為10 t的B型卡車,有10名駕駛員,每輛卡車每天往返的次數為A型卡車4次,B型卡車3次,每輛卡車每天往返的費用為A型卡車320元,B型卡車504元,則公司如何調配車輛,才能使公司所花的費用最低,最低費用為________元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2016·山東)設f(x)=xlnx-ax2+(2a-1)x,a∈R.
(1)令g(x)=f′(x),求g(x)的單調區間;
(2)已知f(x)在x=1處取得極大值,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,焦距為2c,且c,
,焦距為2c,且c, ![]() ,2成等比數列.
,2成等比數列.
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)點B坐標為(0, ![]() ),問是否存在過點B的直線l交橢圓C于M,N兩點,且滿足
),問是否存在過點B的直線l交橢圓C于M,N兩點,且滿足![]() (O為坐標原點)?若存在,求出此時直線l的方程;若不存在,請說明理由.
(O為坐標原點)?若存在,求出此時直線l的方程;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com