Question

【題目】已知圓的圓心在拋物線上，圓過原點且與拋物線的準線相切.

（1）求該拋物線的方程；

（2）過拋物線焦點的直線交拋物線于， 兩點，分別在點， 處作拋物線的兩條切線交于點，求三角形面積的最小值及此時直線的方程.

Answer 1

【答案】(1) ;(2) 三角形PAB面積最小值為4，此時直線L的方程為.

【解析】【試題分析】(1)寫出圓心/半徑,焦點坐標和準線方程,根據原點在圓上及圓心到拋物線的距離建立方程,解方程組求得的值,由此得到拋物線方程.(2)設出直線的方程,聯立直線的方程和拋物線線的方程,寫出韋達定理,利用導數求出切線的方程,求出交點的坐標,利用弦長公式和點到直線距離公式寫出三角形面積的表達式,并由此求得最小值.

【試題解析】

（1）由已知可得圓心，半徑，焦點，準線

因為圓C與拋物線F的準線相切，所以，

且圓C過焦點F，

又因為圓C過原點，所以圓心C必在線段OF的垂直平分線上，

即

所以，即，拋物線F的方程為

（2）易得焦點，直線L的斜率必存在，設為k，即直線方程為

設

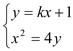得，，

對求導得，即

直線AP的方程為，即，

同理直線BP方程為

設，

聯立AP與BP直線方程解得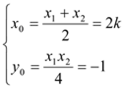，即

所以，點P到直線AB的距離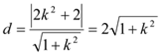

所以三角形PAB面積，當僅當時取等號

綜上：三角形PAB面積最小值為4，此時直線L的方程為.