
【題目】如圖,在直四棱柱![]() 中,底面
中,底面![]() 是邊長為2的正方形,
是邊長為2的正方形, ![]() 分別為線段
分別為線段![]() ,
, ![]() 的中點.
的中點.

(1)求證: ![]() ||平面
||平面![]() ;
;
(2)四棱柱![]() 的外接球的表面積為
的外接球的表面積為![]() ,求異面直線
,求異面直線![]() 與
與![]() 所成的角的大小.
所成的角的大小.
【答案】(1)見解析;(2)![]()
【解析】試題分析:(1)連接BD1,由中位線定理證明EF∥D1B,由線面平行的判定定理證明EF∥平面ABC1D1;
(2)由(1)和異面直線所成角的定義,得異面直線EF與BC所成的角是∠D1BC,由題意和球的表面積公式求出外接球的半徑,由勾股定理求出側棱AA1的長,由直四棱柱的結構特征和線面垂直的定義,判斷出BC⊥CD1,在RT△CC1D1中求出tan∠D1BC,求出∠D1BC可得答案.
試題解析:
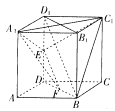
(1)連接![]() ,在
,在![]() 中,
中, ![]() 分別為線段
分別為線段![]() 的中點,∴
的中點,∴![]() 為中位線,
為中位線,
∴![]() ,而
,而![]() 面
面![]() ,
, ![]() 面
面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)由(1)知![]() ,故
,故![]() 即為異面直線
即為異面直線![]() 與
與![]() 所成的角.
所成的角.
∵四棱柱![]() 的外接球的表面積為
的外接球的表面積為![]() ,
,
∴四棱柱![]() 的外接球的半徑
的外接球的半徑![]() ,
,
設![]() ,則
,則![]() ,解得
,解得![]() ,
,
在直四棱柱![]() 中,∵
中,∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() ,在
,在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴異面直線![]() 與
與![]() 所成的角為
所成的角為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() (x
(x![]() R),g(x)=2a-1
R),g(x)=2a-1
(1)求函數f(x)的單調區間與極值.
(2)若f(x)≥g(x)對![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的右焦點為F,上頂點為A,短軸長為2,O為原點,直線AF與橢圓C的另一個交點為B,且△AOF的面積是△BOF的面積的3倍.
=1(a>b>0)的右焦點為F,上頂點為A,短軸長為2,O為原點,直線AF與橢圓C的另一個交點為B,且△AOF的面積是△BOF的面積的3倍.
(1)求橢圓C的方程;
(2)如圖,直線l:y=kx+m與橢圓C相交于P,Q兩點,若在橢圓C上存在點R,使OPRQ為平行四邊形,求m的取值范圍. 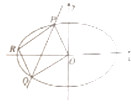
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】全國大學生機器人大賽是由共青團中央,全國學聯,深圳市人民政府聯合主辦的賽事,是中國最具影響力的機器人項目,是全球獨創的機器人競技平臺.全國大學生機器人大賽比拼的是參賽選手們的能力,堅持和態度,展現的是個人實力以及整個團隊的力量.2015賽季共吸引全國240余支機器人戰隊踴躍報名,這些參賽戰隊來自全國六大賽區,150余所高等院校,其中不乏北京大學,清華大學,上海交大,中國科大,西安交大等眾多國內頂尖高校,經過嚴格篩選,最終由111支機器人戰隊參與到2015年全國大學生機器人大賽的激烈角逐之中,某大學共有“機器人”興趣團隊1000個,大一、大二、大三、大四分別有100,200,300,400個,為挑選優秀團隊,現用分層抽樣的方法,從以上團隊中抽取20個團隊.
(1)應從大三抽取多少個團隊?
(2)將20個團隊分為甲、乙兩組,每組10個團隊,進行理論和實踐操作考試(共150分),甲、乙兩組的分數如下:
甲:125,141,140,137,122,114,119,139,121,142
乙:127,116,144,127,144,116,140,140,116,140
從甲、乙兩組中選一組強化訓練,備戰機器人大賽.從統計學數據看,若選擇甲組,理由是什么?若選擇乙組,理由是什么?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱錐A-BCD中,AB⊥平面BCD,CD⊥BD .

(1)求證:CD⊥平面ABD;
(2)若AB=BD=CD=1,M為AD中點,求三棱錐A-MBC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四組函數,表示同一函數的是( )
A.f(x)= ![]() ,g(x)=x
,g(x)=x
B.f(x)=x,g(x)= ![]()
C.f(x)= ![]() ,g(x)=
,g(x)= ![]()
D.(x)=|x+1|,g(x)= ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若關于x的方程x2﹣(a2+b2﹣6b)x+a2+b2+2a﹣4b+1=0的兩個實數根x1 , x2滿足x1≤0≤x2≤1,則a2+b2+4a的最小值和最大值分別為( )
A.![]() 和5+4
和5+4 ![]()
B.﹣ ![]() 和5+4
和5+4 ![]()
C.﹣ ![]() 和12
和12
D.﹣ ![]() 和15﹣4
和15﹣4 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,ABCD是邊長為3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE與平面ABCD所成角為60°. 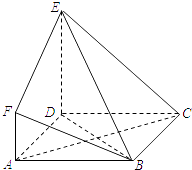
(1)求證:AC⊥平面BDE;
(2)設點M是線段BD上一個動點,試確定點M的位置,使得AM∥平面BEF,并證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com