
【題目】如圖,已知矩形![]() 所在平面與
所在平面與![]() 所在平面互相垂直,
所在平面互相垂直,![]() ,
,![]() .
.

(1)若M為![]() 中點,N為
中點,N為![]() 中點,證明:
中點,證明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,且
,且![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() 的大小.
的大小.
科目:高中數學 來源: 題型:
【題目】關于函數![]() 有下述四個結論:
有下述四個結論:
①![]() 的周期為
的周期為![]() ;
;
②![]() 在
在![]() 上單調遞增;
上單調遞增;
③函數![]() 在
在![]() 上有
上有![]() 個零點;
個零點;
④函數![]() 的最小值為
的最小值為![]() .
.
其中所有正確結論的編號為( )
A.①②B.②③C.③④D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】謝爾賓斯基三角形(Sierpinskitriangle)是由波蘭數學家謝爾賓斯基在1915年提出的,如圖先作一個三角形,挖去一個“中心三角形”(即以原三角形各邊的中點為頂點的三角形),然后在剩下的小三角形中又挖去一個“中心三角形”,我們用白色三角形代表挖去的面積,那么灰色三角形為剩下的面積(我們稱灰色部分為謝爾賓斯基三角形).若通過該種方法把一個三角形挖3次,然后在原三角形內部隨機取一點,則該點取自謝爾賓斯基三角形的概率為______.
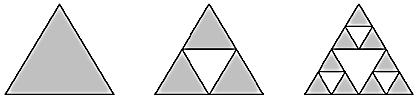
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校在高一部分學生中調查男女同學對某項體育運動的喜好情況,其二維條形圖如圖(黑色代表喜好,白色代表不喜好).
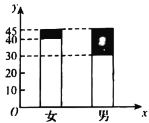
(1)寫出![]() 列聯表;
列聯表;
(2)能否有99%的把握認為喜好這項體育運動與性別有關;
(3)在這次調查中從喜好這項體育活動的一名男生和兩名女生中任選兩人進行專業培訓,求恰是一男一女的概率.
附: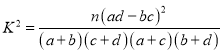
| 0.25 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 的左頂點
的左頂點![]() ,且點
,且點![]() 在橢圓上,
在橢圓上, ![]() 分別是橢圓的左、右焦點。過點
分別是橢圓的左、右焦點。過點![]() 作斜率為
作斜率為![]() 的直線交橢圓
的直線交橢圓![]() 于另一點
于另一點![]() ,直線
,直線![]() 交橢圓
交橢圓![]() 于點
于點![]() .
.
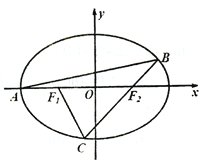
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 為等腰三角形,求點
為等腰三角形,求點![]() 的坐標;
的坐標;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《烏鴉喝水》是《伊索寓言》中一個寓言故事。通過講述一只烏鴉喝水的故事,告訴人們遇到困難要運用智慧、認真思考才能讓問題迎刃而解的道理。如圖2所示,烏鴉想喝水,發現有一個錐形瓶,上面部分是圓柱體,下面部分是圓臺,瓶口直徑為3厘米,瓶底直徑為9厘米,瓶口距瓶頸為![]() 厘米,瓶頸到水位線距離和水位線到瓶底距離均為
厘米,瓶頸到水位線距離和水位線到瓶底距離均為![]() 厘米現將1顆石子投入瓶中,發現水位線上移
厘米現將1顆石子投入瓶中,發現水位線上移![]() 厘米,若只有當水位線到達瓶口時,烏鴉才能喝到水,則烏鴉共需要投入的石子數量至少是?(石子體積均視為一致)
厘米,若只有當水位線到達瓶口時,烏鴉才能喝到水,則烏鴉共需要投入的石子數量至少是?(石子體積均視為一致)
圓臺體積公式:![]() ,其中,
,其中,![]() 為圓臺高,
為圓臺高,![]() 為圓臺下底面半徑,
為圓臺下底面半徑,![]() 為圓臺上底面半徑( )
為圓臺上底面半徑( )


A.2顆B.3顆C.4顆D.5顆
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 中點.將
中點.將![]() 沿
沿![]() 折起到
折起到![]() ,使得平面
,使得平面![]() 平面
平面![]() (如圖2).
(如圖2).

(1)求證:![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ? 若存在,求出
? 若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某客戶準備在家中安裝一套凈水系統,該系統為三級過濾,使用壽命為十年.如圖所示,兩個一級過濾器采用并聯安裝,二級過濾器與三級過濾器為串聯安裝。

其中每一級過濾都由核心部件濾芯來實現。在使用過程中,一級濾芯和二級濾芯都需要不定期更換(每個濾芯是否需要更換相互獨立),三級濾芯無需更換,若客戶在安裝凈水系統的同時購買濾芯,則一級濾芯每個![]() 元,二級濾芯每個
元,二級濾芯每個![]() 元.若客戶在使用過程中單獨購買濾芯,則一級濾芯每個
元.若客戶在使用過程中單獨購買濾芯,則一級濾芯每個![]() 元,二級濾芯每個
元,二級濾芯每個![]() 元。現需決策安裝凈水系統的同時購濾芯的數量,為此參考了根據
元。現需決策安裝凈水系統的同時購濾芯的數量,為此參考了根據![]() 套該款凈水系統在十年使用期內更換濾芯的相關數據制成的圖表,其中圖是根據
套該款凈水系統在十年使用期內更換濾芯的相關數據制成的圖表,其中圖是根據![]() 個一級過濾器更換的濾芯個數制成的柱狀圖,表是根據
個一級過濾器更換的濾芯個數制成的柱狀圖,表是根據![]() 個二級過濾器更換的濾芯個數制成的頻數分布表.
個二級過濾器更換的濾芯個數制成的頻數分布表.

二級濾芯更換頻數分布表
二級濾芯更換的個數 |
|
|
頻數 |
|
|
以![]() 個一級過濾器更換濾芯的頻率代替
個一級過濾器更換濾芯的頻率代替![]() 個一級過濾器更換濾芯發生的概率,以
個一級過濾器更換濾芯發生的概率,以![]() 個二級過濾器更換濾芯的頻率代替
個二級過濾器更換濾芯的頻率代替![]() 個二級過濾器更換濾芯發生的概率.
個二級過濾器更換濾芯發生的概率.
(1)求一套凈水系統在使用期內需要更換的各級濾芯總個數恰好為![]() 的概率;
的概率;
(2)記![]() 表示該客戶的凈水系統在使用期內需要更換的一級濾芯總數,求
表示該客戶的凈水系統在使用期內需要更換的一級濾芯總數,求![]() 的分布列及數學期望;
的分布列及數學期望;
(3)記![]() ,
,![]() 分別表示該客戶在安裝凈水系統的同時購買的一級濾芯和二級濾芯的個數.若
分別表示該客戶在安裝凈水系統的同時購買的一級濾芯和二級濾芯的個數.若![]() ,且
,且![]() ,以該客戶的凈水系統在使用期內購買各級濾芯所需總費用的期望值為決策依據,試確定
,以該客戶的凈水系統在使用期內購買各級濾芯所需總費用的期望值為決策依據,試確定![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知圓C滿足:圓心在
中,已知圓C滿足:圓心在![]() 軸上,且與圓
軸上,且與圓![]() 相外切.設圓C與
相外切.設圓C與![]() 軸的交點為M,N,若圓心C在
軸的交點為M,N,若圓心C在![]() 軸上運動時,在
軸上運動時,在![]() 軸正半軸上總存在定點
軸正半軸上總存在定點![]() ,使得
,使得![]() 為定值,則點
為定值,則點![]() 的縱坐標為_________.
的縱坐標為_________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com