【題目】已知正四棱柱
的底面邊長為2，側棱
，
為上底面
上的動點，給出下列四個結論中正確結論為（ ）
A.若
，則滿足條件的點有且只有一個
B.若
，則點的軌跡是一段圓弧
C.若
∥平面
，則
長的最小值為2
D.若∥平面，且，則平面
截正四棱柱的外接球所得平面圖形的面積為
科目：高中數學 來源： 題型：
【題目】2013年華人數學家張益唐證明了孿生素數猜想的一個弱化形式。孿生素數猜想是希爾伯特在1900年提出的23個問題之一，可以這樣描述：存在無窮多個素數p，使得p+2是素數，素數對(p，p+2)稱為孿生素數．在不超過30的素數中，隨機選取兩個不同的數，其中能夠組成孿生素數的概率是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，四邊形
為梯形， 
，且
， 
是邊長為2的正三角形，頂點
在
上的射影為點
，且
， 
， 
.
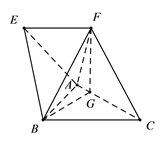
（1）證明：平面
平面
；
（2）求二面角
的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】十九大以來，某貧困地區扶貧辦積極貫徹落實國家精準扶貧的政策要求，帶領廣大農村地區人民群眾脫貧奔小康.經過不懈的奮力拼搏，新農村建設取得巨大進步，農民年收入也逐年增加.為了制定提升農民年收入、實現2020年脫貧的工作計劃，該地扶貧辦統計了2019年50位農民的年收入并制成如下頻率分布直方圖：
（1）根據頻率分布直方圖，估計50位農民的年平均收入
元（單位：千元）（同一組數據用該組數據區間的中點值表示）；
（2）由頻率分布直方圖，可以認為該貧困地區農民年收入X服從正態分布
，其中
近似為年平均收入，
近似為樣本方差
，經計算得
，利用該正態分布，求：
（i）在扶貧攻堅工作中，若使該地區約有占總農民人數的84.14%的農民的年收入高于扶貧辦制定的最低年收入標準，則最低年收入大約為多少千元？
（ii）為了調研“精準扶貧，不落一人”的政策要求落實情況，扶貧辦隨機走訪了1000位農民.若每位農民的年收入互相獨立，問：這1000位農民中的年收入不少于12.14千元的人數最有可能是多少？
附參考數據：
，若隨機變量X服從正態分布，則
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
(a>0，b>0)的左頂點與拋物線y2＝2px(p>0)的焦點的距離為4，且雙曲線的一條漸近線與拋物線的準線的交點坐標為(－2，－1)，則雙曲線的焦距為( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝ex－ax－1（e為自然對數的底數），a＞0．
（1）若函數f（x）恰有一個零點，證明：aa＝ea－1；
（2）若f（x）≥0對任意x∈R恒成立，求實數a的取值集合．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，圓柱的軸截面
是邊長為2的正方形，點
是圓弧
上的一動點（不與
重合），點
是圓弧
的中點，且點
在平面的兩側.
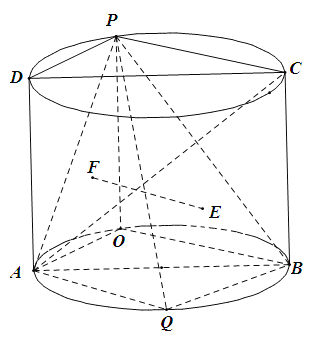
（1）證明：平面
平面
；
（2）設點在平面
上的射影為點
，點
分別是
和
的重心，當三棱錐
體積最大時，回答下列問題.
（ⅰ）證明：
平面
；
（ⅱ）求平面
與平面
所成二面角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
在橢圓
上，
為右焦點，
軸，
為橢圓上的四個動點，且
，
交于原點
.
（1）判斷直線
與橢圓的位置關系；
（2設
，
滿足
，判斷
的值是否為定值，若是，請求出此定值，并求出四邊形
面積的最大值，否則說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
的參數方程為
（
為參數），以平面直角坐標系
的原點
為極點，
軸的正半軸為極軸建立極坐標系，橢圓
的極坐標方程為
.
（1）求直線的普通方程（寫成一般式）和橢圓的直角坐標方程（寫成標準方程）；
（2）若直線與橢圓相交于
，
兩點，且與軸相交于點
，求
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
