【題目】已知函數
，
，
.
（1）若
，求函數
的極小值；
（2）設函數
，求函數
的單調區間；
（3）若在區間
上存在一點
，使得
成立，求
的取值范圍，（
）
【答案】（1）1；（2）詳見解析；（3）：
或
.
【解析】試題分析：（1）
，第一步求函數的導數，第二步求極值點，分析零點兩側的單調性，求得極小值；（2）
， 
，函數的定義域是
，所以討論
和0的大小關系，分
和
兩種情況討論函數的單調性；（3）根據（2）將問題轉化為
，使
，討論極值點
與定義域的關系，分
三種情況討論函數的最小值，令
，求實數
.
試題解析：（1）
的定義域為
，
當
時，
，
，
| （0,1） | 1 |
|
| - | 0 | + |
|
| 極小值 |
|
所以在
處取得極小值1.
（2）
，
，
①當
時，即
時，在
上
，在
上
，
所以
在上單調遞減，在上單調遞增；
②當
，即
時，在上，
所以，函數在上單調遞增.
綜上所述，①當時，的單調遞減區間是，單調遞增區間是；
②當時，函數的單調遞增區間是，不存在減區間.
（3）在
上存在一點
，使得
成立，即
在上存在一點，使得
，即
函數在上的最小值小于零.
由（2）可知
①即
，即
時，在上單調遞減，
所以的最小值為
，由
可得
.
所以；
②當
，即
時，在上單調遞增.
所以最小值為
，由
可得
；
③當
，即
時，可得最小值為
，
因為
，所以，
，
故
，此時，
不成立.
綜上討論可得所求
的范圍是：或.
科目：高中數學 來源： 題型：
【題目】甲、乙兩位射擊運動員，在某天訓練中已各射擊10次，每次命中的環數如下：
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
（Ⅰ）通過計算估計，甲、乙二人的射擊成績誰更穩；
（Ⅱ）若規定命中8環及以上環數為優秀，以頻率作為概率，請依據上述數據估計，求甲在第11至第13次射擊中獲得優秀的次數
的分布列和期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某村電費收取有以下兩種方案供農戶選擇：
方案一：每戶每月收取管理費2元，月用電量不超過30度時，每度0.5元；超過30度時，超過部分按每度0.6元收取；
方案二：不收管理費，每度0.58元．
（1）求方案一
收費（元）與用電量
（度）間的函數關系；
（2）老王家九月份按方案一交費35元，問老王家該月用電多少度？
（3）老王家該月用電量在什么范圍內，選擇方案一比選擇方案二更好？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】關于函數，給出下列命題：
①若函數f(x)是R上周期為3的偶函數，且滿足f(1)＝1，則f(2)－f(－4)＝0；
②若函數f(x)滿足f(x＋1)f(x)＝2 017，則f(x)是周期函數；
③若函數g(x)＝
是偶函數，則f(x)＝x＋1；
④函數y＝
的定義域為
.
其中正確的命題是________.(寫出所有正確命題的序號)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題正確的個數是( )
①命題“x0∈R，x＋1＞3x0”的否定是“x∈R，x2＋1≤3x”；
②“函數f(x)＝cos2ax－sin2ax的最小正周期為π”是“a＝1”的必要不充分條件；
③x2＋2x≥ax在x∈[1,2]上恒成立(x2＋2x)min≥(ax)max在x∈[1,2]上恒成立；
④“平面向量a與b的夾角是鈍角”的充要條件是“a·b＜0”．
A．1 B．2
C．3 D．4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】傾斜角為
的直線
過點P（8,2），直線
和曲線C：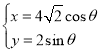
（
為參數）交于不同的兩點M1、M2.
（1）將曲線C的參數方程化為普通方程，并寫出直線
的參數方程；
（2）求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
， 
.
（1）求函數
在
的最小值；
（2）若函數
與
的圖象恰有一個公共點，求實數
的值；
（3）若函數
有兩個不同的極值點
，且
，求實數
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
