
【題目】選修![]() :不等式選講
:不等式選講
已知函數f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若關于x的不等式f(x)≤|3m+1|有解,求實數m的取值范圍.
【答案】(1)![]() (2)m≤﹣
(2)m≤﹣![]() 或m≥1.
或m≥1.
【解析】試題分析:(Ⅰ)分三種情況討論,分別求解不等式組,然后求并集即可得結果;(Ⅱ)原不等式等價于f(x)min≤|3m+1|,求出![]() 的最小值,解關于
的最小值,解關于![]() 的不等式,即可得結果.
的不等式,即可得結果.
試題解析:解:(Ⅰ)不等式f(x)<8,即|2x+3|+|2x﹣1|<8,
可化為①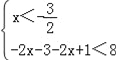 或②
或②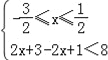 或③
或③ ,…
,…
解①得﹣![]() <x<﹣
<x<﹣![]() ,解②得﹣
,解②得﹣![]() ≤x≤
≤x≤![]() ,解③得
,解③得![]() <x<
<x<![]() ,
,
綜合得原不等式的解集為{x|-![]() }.
}.
(Ⅱ)因為∵f(x)=|2x+3|+|2x﹣1|≥|(2x+3)﹣(2x﹣1)|=4,
當且僅當﹣![]() ≤x≤
≤x≤![]() 時,等號成立,即f(x)min=4,…
時,等號成立,即f(x)min=4,…
又不等式f(x)≤|3m+1|有解,則|3m+1|≥4,解得:m≤﹣![]() 或m≥1.
或m≥1.


科目:高中數學 來源: 題型:
【題目】已知坐標平面上點![]() 與兩個定點
與兩個定點![]() ,
, ![]() 的距離之比等于5.
的距離之比等于5.
(1)求點![]() 的軌跡方程,并說明軌跡是什么圖形;
的軌跡方程,并說明軌跡是什么圖形;
(2)記(1)中的軌跡為![]() ,過點
,過點![]() 的直線
的直線![]() 被
被![]() 所截得的線段的長為 8,求直線
所截得的線段的長為 8,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知p:指數函數f(x)=(2a-6)x在R上是單調減函數;q:關于x的方程x2-3ax+2a2+1=0的兩根均大于3,若p或q為真,p且q為假,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題,其中正確的序號是__________________(寫出所有正確命題的序號)
①函數![]() 的圖像恒過定點
的圖像恒過定點![]() ;
;
②已知集合![]() ,則映射
,則映射![]() 中滿足
中滿足![]() 的映射共有1個;
的映射共有1個;
③若函數![]() 的值域為R,則實數
的值域為R,則實數![]() 的取值范圍是
的取值范圍是![]() ;
;
④函數![]() 的圖像關于
的圖像關于![]() 對稱的函數解析式為
對稱的函數解析式為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數![]() 是奇函數
是奇函數
(1)求![]() 的值
的值
(2)判斷f(x)在![]() 上的單調性。(直接寫出答案,不用證明)
上的單調性。(直接寫出答案,不用證明)
(3)若對于任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x-1|+|x+1|(x∈R).
(1)證明:函數f(x)是偶函數;
(2)利用絕對值及分段函數知識,將函數解析式寫成分段函數的形式,然后畫出函數圖象;
(3)寫出函數的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】羅源濱海新城建一座橋,兩端的橋墩已建好,這兩墩相距![]() 米,余下工程只需建兩端橋墩之間的橋面和橋墩,經預測,一個橋墩的工程費用為32萬元,距離為x米的相鄰兩墩之間的橋面工程費用為
米,余下工程只需建兩端橋墩之間的橋面和橋墩,經預測,一個橋墩的工程費用為32萬元,距離為x米的相鄰兩墩之間的橋面工程費用為![]() 萬元.假設橋墩等距離分布,所有橋墩都視為點,且不考慮其他因素,記余下工程的費用為
萬元.假設橋墩等距離分布,所有橋墩都視為點,且不考慮其他因素,記余下工程的費用為![]() 萬元.
萬元.
(1)試寫出![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)當![]() =96米,需新建多少個橋墩才能使余下工程的費用
=96米,需新建多少個橋墩才能使余下工程的費用![]() 最小?
最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
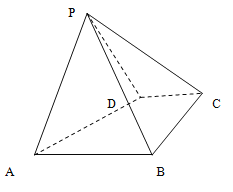
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,側面
,側面![]() 底面
底面![]() ,且
,且![]() 是以
是以![]() 為底的等腰三角形.
為底的等腰三角形.
(Ⅰ)證明:![]()
(Ⅱ)若四棱錐![]() 的體積等于
的體積等于![]() .問:是否存在過點
.問:是否存在過點![]() 的平面
的平面![]() 分別交
分別交![]() ,
,![]() 于點
于點![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的面積;若不存在,請說明理由.
的面積;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com