
【題目】給出下列命題:
(1)終邊在y軸上的角的集合是![]() ;
;
(2)把函數f(x)=2sin2x的圖象沿x軸方向向左平移![]() 個單位后,得到的函數解析式可以表示成f(x)=2sin
個單位后,得到的函數解析式可以表示成f(x)=2sin![]() ;
;
(3)函數f(x)=![]() sinx+
sinx+![]() 的值域是[-1,1];
的值域是[-1,1];
(4)已知函數f(x)=2cosx,若存在實數x1,x2,使得對任意的實數x都有![]() 成立,則
成立,則![]() 的最小值為2π.
的最小值為2π.
其中正確的命題的序號為________.
科目:高中數學 來源: 題型:
【題目】已知一個圓經過坐標原點和點(2,0),且圓心C在直線y=2x上.
(1)求圓C的方程;
(2)過點P(-2,2)作圓C的切線PA和PB,求直線PA和PB的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位安排7位員工對一周的7個夜晚值班,每位員工值一個夜班且不重復值班,其中員工甲必須安排在星期一或星期二值班,員工乙不能安排在星期二值班,員工丙必須安排在星期五值班,則這個單位安排夜晚值班的方案共有( )
A. 96種B. 144種C. 200種D. 216種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“日行一萬步,健康你一生”的養生觀念已經深入人心,由于研究性學習的需要,某大學生收集了手機“微信運動”團隊中特定甲、乙兩個班級![]() 名成員一天行走的步數,然后采用分層抽樣的方法按照
名成員一天行走的步數,然后采用分層抽樣的方法按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 分層抽取了20名成員的步數,并繪制了如下尚不完整的莖葉圖(單位:千步):
分層抽取了20名成員的步數,并繪制了如下尚不完整的莖葉圖(單位:千步):

已知甲、乙兩班行走步數的平均值都是44千步.
(1)求![]() 的值;
的值;
(2)(ⅰ)若![]() ,求甲、乙兩個班級100名成員中行走步數在
,求甲、乙兩個班級100名成員中行走步數在![]() ,
, ![]() ,
, ![]() ,
, ![]() 各層的人數;
各層的人數;
(ⅱ)若估計該團隊中一天行走步數少于40千步的人數比處于![]() 千步的人數少12人,求
千步的人數少12人,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的直角坐標方程及曲線
的直角坐標方程及曲線![]() 的普通方程;
的普通方程;
(2)設![]() 是曲線
是曲線![]() 上的一動點,求
上的一動點,求![]() 到直線
到直線![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“雙十一”期間,某淘寶店主對其商品的上架時間![]() (小時)和銷售量
(小時)和銷售量![]() (件)的關系作了統計,得到了如下數據并研究.
(件)的關系作了統計,得到了如下數據并研究.
上架時間 | 2 | 4 | 6 | 8 | 10 | 12 |
銷售量 | 64 | 138 | 205 | 285 | 360 | 430 |
(1)求表中銷售量![]() 的平均數和中位數;
的平均數和中位數;
(2)① 作出散點圖,并判斷變量![]() 與
與![]() 是否線性相關?若研究的方案是先根據前5組數據求線性回歸方程,再利用第6組數據進行檢驗,求線性回歸方程
是否線性相關?若研究的方案是先根據前5組數據求線性回歸方程,再利用第6組數據進行檢驗,求線性回歸方程![]() ;
;
②若根據①中線性回歸方程得到商品上架12小時的銷售量的預測值與檢測值不超過3件,則認為得到的線性回歸方程是理想的,試問:①中的線性回歸方程是否理想.
附:線性回歸方程![]() 中,
中, 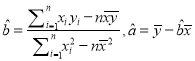 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知![]() ,
, ![]() 分別為橢圓
分別為橢圓![]() :
: ![]() 的上、下焦點,
的上、下焦點, ![]() 是拋物線
是拋物線![]() :
: ![]() 的焦點,點
的焦點,點![]() 是
是![]() 與
與![]() 在第二象限的交點,且
在第二象限的交點,且![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)與圓![]() 相切的直線
相切的直線![]() :
: ![]() (其中
(其中![]() )交橢圓
)交橢圓![]() 于點
于點![]() ,
, ![]() ,若橢圓
,若橢圓![]() 上一點
上一點![]() 滿足
滿足![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com