Question

【題目】海安市江淮文化園是以江淮歷史文化為底蘊的人文景觀，整個園區由白龍故里、先賢景區、鳳山書院、中國名人藝術館群四大景區組成．據估計，其中鳳山書院景區每天的水電、人工等固定成本為1000元，另每增加一名游客需另外增加成本10元，鳳山書院景區門票單價x（元）（x∈N*）與日門票銷售量（張）的關系如下表，并保證鳳山書院景區每天盈利．

x	20	35	40	50
y	400	250	200	100

（1）在坐標圖紙中，根據表中提供的數據，描出實數對的對應點，并確定y與x的函數關系式；

（2）求出的值，并解釋其實際意義；

（3）請寫出鳳山書院景區的日利潤的表達式，并回答該景區怎樣定價才能獲最大日利潤？

Answer 1

【答案】（1） ； （2）銷售單價每上漲1元，日銷售量減少10張；（3） （N*），當時，有最大值，故單價定為元時，才能獲得日最大利潤．

【解析】

（1）由題表作出四點的對應點，它們分布在一條直線上，據此可得函數解析式為（N*）．

（2）由（1）可得，然后解釋其實際意義即可；

（3）由題意求得函數的解析式，然后結合二次函數的性質討論該景區怎樣定價才能獲最大日利潤即可.

（1）由題表在坐標紙中作出四點的對應點如圖所示，它們分布在一條直線上，

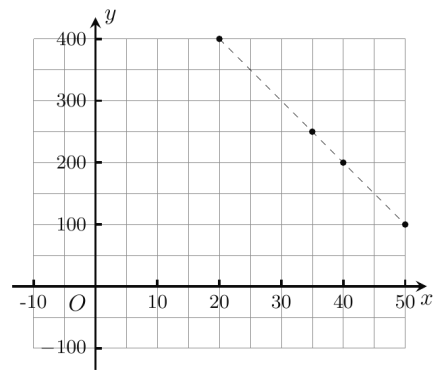
設它們共線于，則取兩點的坐標代入得：

.

所以（N*），

經檢驗，也在此直線上．

故所求函數解析式為（N*）．

（2）由（1）可得，實際意義表示：銷售單價每上漲1元，日銷售量減少10張．

（3）依題意: （N*）圖象開口向下，對稱軸為.

當時，函數單調遞增；當時，函數單調遞減. 故當時，有最大值，答：當時，有最大值，故單價定為元時，才能獲得日最大利潤．