
【題目】已知中心在原點(diǎn)的橢圓![]() 的兩焦點(diǎn)分別為雙曲線(xiàn)
的兩焦點(diǎn)分別為雙曲線(xiàn)![]() 的頂點(diǎn),直線(xiàn)
的頂點(diǎn),直線(xiàn)![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點(diǎn),且
兩點(diǎn),且![]() ,點(diǎn)
,點(diǎn)![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 、
、![]() 的任意一點(diǎn),直線(xiàn)
的任意一點(diǎn),直線(xiàn)![]() 外的點(diǎn)
外的點(diǎn)![]() 滿(mǎn)足
滿(mǎn)足![]() ,
, ![]() .
.
(1)求點(diǎn)![]() 的軌跡方程;
的軌跡方程;
(2)試確定點(diǎn)![]() 的坐標(biāo),使得
的坐標(biāo),使得![]() 的面積最大,并求出最大面積.
的面積最大,并求出最大面積.
【答案】(1)見(jiàn)解析;(2)![]() 或
或![]()
【解析】
(1)先求出橢圓的方程為![]() ,
,![]() .令點(diǎn)
.令點(diǎn)![]() ,
, ![]() ,再根據(jù)
,再根據(jù)![]() ,
, ![]() 求出點(diǎn)
求出點(diǎn)![]() 的軌跡方程.(2)先求出點(diǎn)
的軌跡方程.(2)先求出點(diǎn)![]() 到直線(xiàn)
到直線(xiàn)![]()
![]() 的距離
的距離![]() ,
, ![]() ,
,![]() ,再利用重要不等式求函數(shù)的最大值和點(diǎn)Q的坐標(biāo).
,再利用重要不等式求函數(shù)的最大值和點(diǎn)Q的坐標(biāo).
(1)由![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() 的頂點(diǎn),得
的頂點(diǎn),得![]() 的焦點(diǎn)
的焦點(diǎn)![]()
![]() ,
, ![]() .
.
令![]() 的方程為
的方程為![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() 在
在![]() 上,所以
上,所以![]() .
.
于是由![]() 解得
解得![]() ,
, ![]() ,所以
,所以![]() 的方程為
的方程為![]() .
.
由直線(xiàn)![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點(diǎn),知
兩點(diǎn),知![]() 、
、![]() 關(guān)于原點(diǎn)對(duì)稱(chēng),所以
關(guān)于原點(diǎn)對(duì)稱(chēng),所以![]() .
.
令點(diǎn)![]() ,
, ![]() ,則
,則![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
于是由![]() ,
, ![]() ,得
,得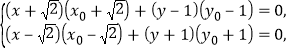
即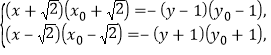
兩式相乘得![]() .
.
又因?yàn)辄c(diǎn)![]() 在
在![]() 上,所以
上,所以![]() ,即
,即![]() ,
,
代入![]() 中,得
中,得![]()
![]() .
.
當(dāng)![]() 時(shí),得
時(shí),得![]() ;
;
當(dāng)![]() 時(shí),則點(diǎn)
時(shí),則點(diǎn)![]() 或
或![]() ,此時(shí)
,此時(shí)![]() 或
或![]() ,也滿(mǎn)足方程
,也滿(mǎn)足方程![]() .
.
若點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合,即
重合,即![]() 時(shí),由
時(shí),由![]() 解得
解得![]() 或
或![]() .
.
若點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時(shí),同理可得
重合時(shí),同理可得![]() 或
或![]() .
.
綜上,點(diǎn)![]() 的軌跡是橢圓
的軌跡是橢圓![]() 除去四個(gè)點(diǎn)
除去四個(gè)點(diǎn)![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其方程為
,其方程為![]() (
(![]() ,
, ![]() ).
).
(2)因?yàn)辄c(diǎn)![]() 到直線(xiàn)
到直線(xiàn)![]()
![]() 的距離
的距離![]() ,
, ![]() ,
,
所以![]() 的面積
的面積![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
當(dāng)且僅當(dāng)![]() ,即
,即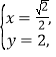 或
或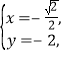
![]() ,
,
此時(shí)點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() 或
或![]() .
.


 世紀(jì)百通期末金卷系列答案
世紀(jì)百通期末金卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】
在平面直角坐標(biāo)系中,以坐標(biāo)原點(diǎn)為極點(diǎn),x軸的非負(fù)半軸為極軸建立極坐標(biāo)系.已知點(diǎn)A的極坐標(biāo)(![]() ,
,![]() ),直線(xiàn)l的極坐標(biāo)方程為ρcos(θ-
),直線(xiàn)l的極坐標(biāo)方程為ρcos(θ-![]() )=a,.
)=a,.
(1)若點(diǎn)A在直線(xiàn)l上,求直線(xiàn)l的直角坐標(biāo)方程;
(2)圓C的參數(shù)方程為![]() (
(![]() 為參數(shù)),若直線(xiàn)
為參數(shù)),若直線(xiàn)![]() 與圓C相交的弦長(zhǎng)為
與圓C相交的弦長(zhǎng)為![]() ,求
,求![]() 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() .
.
(1)求函數(shù)y=f(x)圖象的對(duì)稱(chēng)軸方程;
(2)求函數(shù)h(x)=f(x)+g(x)的最小正周期和值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)的定義域?yàn)椋?/span>﹣∞,0)∪(0,+∞),f(x)是奇函數(shù),且當(dāng)x>0時(shí),f(x)=x2﹣x+a,若函數(shù)g(x)=f(x)﹣x的零點(diǎn)恰有兩個(gè),則實(shí)數(shù)a的取值范圍是( )
A.a<0B.a≤0C.a≤1D.a≤0或a=1
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
已知極坐標(biāo)系的極點(diǎn)在平面直角坐標(biāo)系的原點(diǎn)![]() 處,極軸與
處,極軸與![]() 軸的正半軸重合,且長(zhǎng)度單位相同;曲線(xiàn)
軸的正半軸重合,且長(zhǎng)度單位相同;曲線(xiàn)![]() 的方程是
的方程是![]() ,直線(xiàn)
,直線(xiàn)![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù),
為參數(shù),![]() ),設(shè)
),設(shè)![]() , 直線(xiàn)
, 直線(xiàn)![]() 與曲線(xiàn)
與曲線(xiàn)![]() 交于
交于 ![]() 兩點(diǎn).
兩點(diǎn).
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 的長(zhǎng)度;
的長(zhǎng)度;
(2)求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】國(guó)家質(zhì)量監(jiān)督檢驗(yàn)檢疫局于2004年5月31日發(fā)布了新的《車(chē)輛駕駛?cè)藛T血液、呼吸酒精含量閥值與檢驗(yàn)》國(guó)家標(biāo)準(zhǔn),新標(biāo)準(zhǔn)規(guī)定,車(chē)輛駕駛?cè)藛T血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫克升為飲酒駕車(chē),血液中的酒精含量大于或等于80毫克/百毫升為醉酒駕車(chē),經(jīng)過(guò)反復(fù)試驗(yàn),喝1瓶啤酒后酒精在人體血液中的變化規(guī)律的“散點(diǎn)圖”如下:
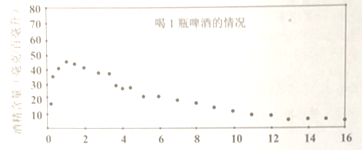
該函數(shù)模型如下:
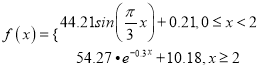
根據(jù)上述條件,回答以下問(wèn)題:
(1)試計(jì)算喝1瓶啤酒后多少小時(shí)血液中的酒精含量達(dá)到最大值?最大值是多少?
(2)試計(jì)算喝1瓶啤酒后多少小時(shí)后才可以駕車(chē)?(時(shí)間以整小時(shí)計(jì)算)
(參數(shù)數(shù)據(jù): ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,正方體![]() 的棱長(zhǎng)為
的棱長(zhǎng)為![]() ,
,![]() ,
,![]() 是線(xiàn)段
是線(xiàn)段![]() 上的兩個(gè)動(dòng)點(diǎn),且
上的兩個(gè)動(dòng)點(diǎn),且![]() ,則下列結(jié)論錯(cuò)誤的是 ( )
,則下列結(jié)論錯(cuò)誤的是 ( )
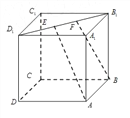
A. ![]()
B. 直線(xiàn)![]() 、
、![]() 所成的角為定值
所成的角為定值
C. ![]() ∥平面
∥平面![]()
D. 三棱錐![]() 的體積為定值
的體積為定值
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(1)從偶函數(shù)的定義出發(fā),證明函數(shù)![]() 是偶函數(shù)的充要條件是它的圖象關(guān)于y軸對(duì)稱(chēng);
是偶函數(shù)的充要條件是它的圖象關(guān)于y軸對(duì)稱(chēng);
(2)從奇函數(shù)的定義出發(fā),證明函數(shù)![]() 是奇函數(shù)的充要條件是它的圖象關(guān)于原點(diǎn)對(duì)稱(chēng).
是奇函數(shù)的充要條件是它的圖象關(guān)于原點(diǎn)對(duì)稱(chēng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】空氣質(zhì)量指數(shù)AQI是反映空氣質(zhì)量狀況的指數(shù),AQI指數(shù)值越小,表明空氣質(zhì)量越好,其對(duì)應(yīng)關(guān)系如下表:
AQI指數(shù)值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空氣質(zhì)量 | 優(yōu) | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴(yán)重污染 |
下圖是某市10月1日—20日AQI指數(shù)變化趨勢(shì):

下列敘述錯(cuò)誤的是
A. 這20天中AQI指數(shù)值的中位數(shù)略高于100
B. 這20天中的中度污染及以上的天數(shù)占![]()
C. 該市10月的前半個(gè)月的空氣質(zhì)量越來(lái)越好
D. 總體來(lái)說(shuō),該市10月上旬的空氣質(zhì)量比中旬的空氣質(zhì)量好
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com