
【題目】2018年8月18日,舉世矚目的第18屆亞運會在印尼首都雅加達(dá)舉行,為了豐富亞運會志愿者的業(yè)余生活,同時鼓勵更多的有志青年加入志愿者行列,大會主辦方?jīng)Q定對150名志愿者組織一次有關(guān)體育運動的知識競賽(滿分120分)并計劃對成績前15名的志愿者進(jìn)行獎勵,現(xiàn)將所有志愿者的競賽成績制成頻率分布直方圖,如圖所示,若第三組與第五組的頻數(shù)之和是第二組的頻數(shù)的3倍,試回答以下問題:
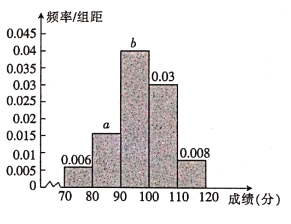
(1)求圖中![]() 的值;
的值;
(2)求志愿者知識競賽的平均成績;
(3)從受獎勵的15人中按成績利用分層抽樣抽取5人,再從抽取的5人中,隨機(jī)抽取2人在主會場服務(wù),求抽取的這2人中其中一人成績在![]() 分的概率.
分的概率.
【答案】(1)![]() (2)96.8(3)
(2)96.8(3)![]()
【解析】
(1)由頻率分布直方圖的性質(zhì)結(jié)合條件即可求解;
(2)每個小長方形底邊中點所對應(yīng)的橫坐標(biāo)乘以該組的頻率,再求和即可求出平均數(shù);
(3)用列舉法先求出從抽取的5人中,隨機(jī)抽取2人所包含的基本事件總數(shù),以及抽取的這2人中其中一人成績在![]() 分所包含的基本事件個數(shù),結(jié)合古典概型的概率公式即可求出概率.
分所包含的基本事件個數(shù),結(jié)合古典概型的概率公式即可求出概率.
(1)由條件及頻率分別直方圖的性質(zhì)可知:![]()
解得![]()
(2)由(1)可知,成績在![]() 分的有9人,在
分的有9人,在![]() 分的有24人,
分的有24人,
在![]() 分的有60人,在
分的有60人,在![]() 分的有45人,
分的有45人,
在![]() 分的有12人,故志愿者知識競賽平均成績?yōu)?/span>
分的有12人,故志愿者知識競賽平均成績?yōu)?/span>![]()
(3)由(2)可知,受獎勵的15人中有三人的成績是![]() 分,其余12人的成績是
分,其余12人的成績是![]() 分,利用分層抽樣抽取5人,有1人成績在
分,利用分層抽樣抽取5人,有1人成績在![]() 分中,4人成績在
分中,4人成績在![]() 分中.
分中.
記成績是![]() 分的1人為
分的1人為![]() ,成績是
,成績是![]() 分的4人為
分的4人為![]() ,從這5人中抽取2人去主會場服務(wù)共有以下10種可能:
,從這5人中抽取2人去主會場服務(wù)共有以下10種可能:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
滿足條件的有![]() ,
,![]() ,
,![]() ,
,![]() ,共4種,
,共4種,
故所求概率![]() .
.


 導(dǎo)學(xué)與測試系列答案
導(dǎo)學(xué)與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,g(x)=f(x)﹣3.
,g(x)=f(x)﹣3.
(1)判斷并證明函數(shù)g(x)的奇偶性;
(2)判斷并證明函數(shù)g(x)在(1,+∞)上的單調(diào)性;
(3)若f(m2﹣2m+7)≥f(2m2﹣4m+4)成立,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() 為
為![]() 的導(dǎo)函數(shù).
的導(dǎo)函數(shù).
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 在
在![]() 上存在最大值0,求函數(shù)
上存在最大值0,求函數(shù)![]() 在
在![]() 上的最大值;
上的最大值;
(3)求證:當(dāng)![]() 時,
時,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某機(jī)構(gòu)為了解某地區(qū)中學(xué)生在校月消費情況,隨機(jī)抽取了 100名中學(xué)生進(jìn)行調(diào)查.如圖是根據(jù)調(diào)査的結(jié)果繪制的學(xué)生在校月消費金額的頻率分布直方圖.已知![]() 三個金額段的學(xué)生人數(shù)成等差數(shù)列,將月消費金額不低于550元的學(xué)生稱為“高消費群”.
三個金額段的學(xué)生人數(shù)成等差數(shù)列,將月消費金額不低于550元的學(xué)生稱為“高消費群”.
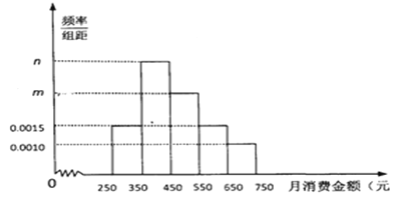
(1)求![]() 的值,并求這100名學(xué)生月消費金額的樣本平均數(shù)
的值,并求這100名學(xué)生月消費金額的樣本平均數(shù)![]() (同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表);
(同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表);
(2)根據(jù)已知條件完成下面![]() 列聯(lián)表,并判斷能否有
列聯(lián)表,并判斷能否有![]() 的把握認(rèn)為“高消費群”與性別有關(guān)?
的把握認(rèn)為“高消費群”與性別有關(guān)?

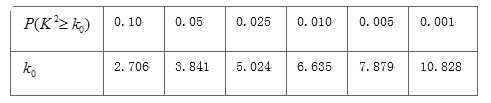
附: ![]() (其中
(其中![]() 樣本容量)
樣本容量)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}的前n項和為Sn,滿足Sn=2an-1(n∈N*),數(shù)列{bn}滿足nbn+1-(n+1)bn=n(n+1)(n∈N*),且b1=1.
(1)證明數(shù)列{![]() }為等差數(shù)列,并求數(shù)列{an}和{bn}的通項公式;
}為等差數(shù)列,并求數(shù)列{an}和{bn}的通項公式;
(2)若cn=(-1)n-1![]() ,求數(shù)列{cn}的前n項和T2n;
,求數(shù)列{cn}的前n項和T2n;
(3)若dn=an![]() ,數(shù)列{dn}的前n項和為Dn,對任意的n∈N*,都有Dn≤nSn-a,求實數(shù)a的取值范圍.
,數(shù)列{dn}的前n項和為Dn,對任意的n∈N*,都有Dn≤nSn-a,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】由無理數(shù)引發(fā)的數(shù)學(xué)危機(jī)一直延續(xù)到19世紀(jì).直到1872年,德國數(shù)學(xué)家戴德金從連續(xù)性的要求出發(fā),用有理數(shù)的“分割”來定義無理數(shù)(史稱戴德金分割),并把實數(shù)理論建立在嚴(yán)格的科學(xué)基礎(chǔ)上,才結(jié)束了無理數(shù)被認(rèn)為“無理”的時代,也結(jié)束了持續(xù)2000多年的數(shù)學(xué)史上的第一次大危機(jī).所謂戴德金分割,是指將有理數(shù)集![]() 劃分為兩個非空的子集
劃分為兩個非空的子集![]() 與
與![]() ,且滿足
,且滿足![]() ,
,![]() ,
,![]() 中的每一個元素都小于
中的每一個元素都小于![]() 中的每一個元素,則稱
中的每一個元素,則稱![]() 為戴德金分割.試判斷,對于任一戴德金分割
為戴德金分割.試判斷,對于任一戴德金分割![]() ,下列選項中,不可能成立的是()
,下列選項中,不可能成立的是()
A.![]() 沒有最大元素,
沒有最大元素, ![]() 有一個最小元素B.
有一個最小元素B.![]() 沒有最大元素,
沒有最大元素, ![]() 也沒有最小元素
也沒有最小元素
C.![]() 有一個最大元素,
有一個最大元素, ![]() 有一個最小元素D.
有一個最小元素D.![]() 有一個最大元素,
有一個最大元素, ![]() 沒有最小元素
沒有最小元素
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方體![]() 中,點
中,點![]() ,
,![]() 分別為棱
分別為棱![]() ,
,![]() 的中點,點
的中點,點![]() 為上底面的中心,過
為上底面的中心,過![]() ,
,![]() ,
,![]() 三點的平面把正方體分為兩部分,其中含
三點的平面把正方體分為兩部分,其中含![]() 的部分為
的部分為![]() ,不含
,不含![]() 的部分為
的部分為![]() ,連結(jié)
,連結(jié)![]() 和
和![]() 的任一點
的任一點![]() ,設(shè)
,設(shè)![]() 與平面
與平面![]() 所成角為
所成角為![]() ,則
,則![]() 的最大值為
的最大值為

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】兩個人射擊,甲射擊一次中靶概率是![]() ,乙射擊一次中靶概率是
,乙射擊一次中靶概率是![]() .
.
(1)兩人各射擊一次,中靶至少一次就算完成目標(biāo),則完成目標(biāo)概率是多少?
(2)兩人各射擊2次,中靶至少3次就算完成目標(biāo),則完成目標(biāo)的概率是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】通過市場調(diào)查,得到某種產(chǎn)品的資金投入x(單位:萬元)與獲得的利潤y(單位:萬元)的數(shù)據(jù),如表所示:
資金投入x | 2 | 3 | 4 | 5 | 6 |
利潤y | 2 | 3 | 5 | 6 | 9 |
(1)畫出數(shù)據(jù)對應(yīng)的散點圖;
(2)根據(jù)上表提供的數(shù)據(jù),用最小二乘法求線性回歸直線方程![]() ;
;
(3)現(xiàn)投入資金10萬元,求獲得利潤的估計值為多少萬元?
參考公式:
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com