Question

【題目】如圖，已知正方形ABCD和矩形ACEF中，AB＝，CE＝1，CE⊥平面ABCD．

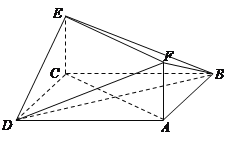
（1）求異面直線DF與BE所成角的余弦值；

（2）求二面角A－DF－B的大小．

Answer 1

【答案】（1）；（2）．

【解析】分析：（1）建立空間直角坐標系，利用向量法求異面直線DF與BE所成角的余弦值.(2)利用向量法求二面角A－DF－B的大小.

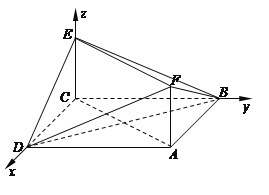
詳解：⑴以{ }為正交基底，建立如圖空間直角坐標系C－xyz，

則D(，0，0)，F(，，1)，E(0，0，1)，B(0，，0)，C(0，0，0)，

所以＝(0，，1)，＝(0，–，1)，

從而cos<， >＝．

所以直線DF與BE所成角的余弦值為．

(2)平面ADF的法向量為＝ (，0，0).

設面BDF的法向量為 = (x，y，z)．又＝(，0，1)．

由 ＝0，＝0，

得y＋z＝0， x＋z＝0

取x＝1，則y＝1，z＝–，所以= (1，1，－)，

所以cos<>＝．

又因為<>∈[0，]，所以<>＝．

所以二面角A – DF – B的大小為．