
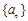 的前n項和為
的前n項和為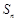 ,
,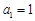 ,且
,且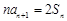 (
(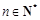 ),數列
),數列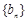 滿足
滿足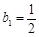 ,
,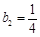 ,對任意
,對任意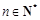 ,都有
,都有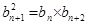 。
。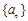 、
、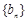 的通項公式;
的通項公式;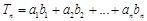 .
.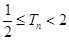 ;
;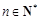 ,不等式
,不等式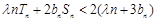 恒成立,試求實數λ的取值范圍.
恒成立,試求實數λ的取值范圍.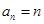 ,
,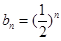 ;(2)
;(2)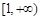 。
。 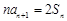 利用
利用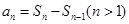 求出數列
求出數列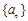 的遞推關系式,再利用累乘法數列
的遞推關系式,再利用累乘法數列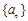 的通項公式;(2)利用錯位相減法求出
的通項公式;(2)利用錯位相減法求出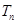 ,易知
,易知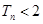 ,再根據數列的單調性可知
,再根據數列的單調性可知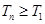 ;
; 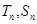 代入
代入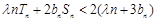 整理得
整理得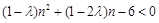 ,然后參變量分離
,然后參變量分離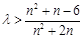 ,構造函數
,構造函數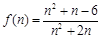 ,求
,求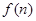 的最大值,或者是直接構造函數
的最大值,或者是直接構造函數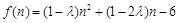 ,然后對二次項系數進行討論,轉化為求二次函數最值問題。
,然后對二次項系數進行討論,轉化為求二次函數最值問題。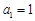 ,
,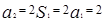
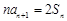 ,∴
,∴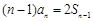 (
(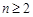 ),
),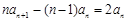 (
(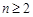 )
)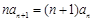 ,即
,即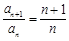 (
( 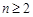 ),
), 
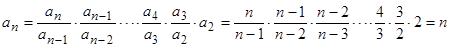 (
(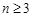 ),
),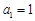 ,
,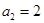 也滿足上式,故數列
也滿足上式,故數列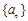 的通項公式
的通項公式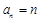 (
(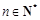 )。
)。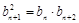 ,知數列
,知數列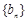 是等比數列,其首項、公比均為
是等比數列,其首項、公比均為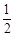 ,
,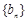 的通項公式
的通項公式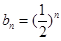 。
。 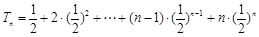 ①
①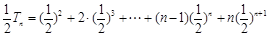 ②
②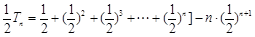
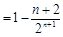 ,
,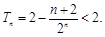
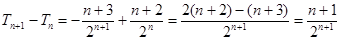 恒正,
恒正,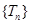 是遞增數列,
是遞增數列,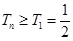 , ∴
, ∴ 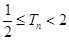 。
。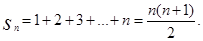 不等式
不等式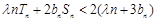
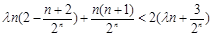 ,即
,即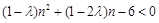 (
(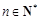 )恒成立.
)恒成立.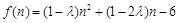 (
(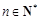 ),
),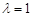 時,
時, 恒成立,則
恒成立,則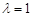 滿足條件;
滿足條件; 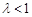 時,由二次函數性質知不恒成立;
時,由二次函數性質知不恒成立; 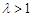 時,由于對稱軸
時,由于對稱軸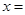

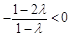 ,則
,則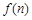 在
在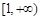 上單調遞減,
上單調遞減,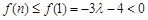 恒成立,則
恒成立,則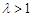 滿足條件,
滿足條件, 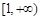 。
。 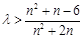 (
(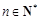 )恒成立,
)恒成立, 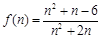 .則
.則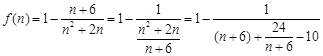 ,
, 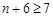 ,
,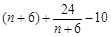 單調遞增且大于0,∴
單調遞增且大于0,∴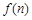 單調遞增,
單調遞增,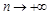 時,
時,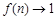 ,且
,且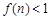 ,故
,故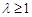 ,∴實數λ的取值范圍是
,∴實數λ的取值范圍是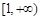 。
。 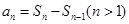 及累乘法求數列的通項公式;(2)利用錯位相減法進行數列求和;(3)數列單調性的判斷;(4)構造函數解決不等式恒成立問題。
及累乘法求數列的通項公式;(2)利用錯位相減法進行數列求和;(3)數列單調性的判斷;(4)構造函數解決不等式恒成立問題。

 星級口算天天練系列答案
星級口算天天練系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com