
已知函數f(x)=x3﹣x2+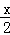 +
+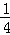 ,且存在x0∈(0,
,且存在x0∈(0,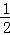 ),使f(x0)=x0.
),使f(x0)=x0.
(1)證明:f(x)是R上的單調增函數;
(2)設x1=0,xn+1=f(xn);y1=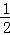 ,yn+1=f(yn),其中n=1,2,…,證明:xn<xn+1<x0<yn+1<yn;
,yn+1=f(yn),其中n=1,2,…,證明:xn<xn+1<x0<yn+1<yn;
(3)證明: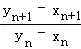 <
<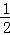 .
.
(1)見解析;(2)見解析;(3)見解析
【解析】
試題分析:(1)證明函數f(x)在R上的單調增,只需證其導函數在R上恒大于零即可;
(2)先驗證n=1時是否成立,假設當n=k(k≥1)時有xk<xk+1<x0<yk+1<yk,再驗證n=k+1時是否成立;
(3)利用基本不等式進行化簡,利用整體的思想轉化成二次函數,再根據二次函數性質求函數的最值即可.
【解析】
(1)∵f'(x)=3x2﹣2x+ =3(x﹣
=3(x﹣ )2+
)2+ >0,
>0,
∴f(x)是R上的單調增函數.
(2)∵0<x0< ,即x1<x0<y1.又f(x)是增函數,
,即x1<x0<y1.又f(x)是增函數,
∴f(x1)<f(x0)<f(y1).即x2<x0<y2.
又x2=f(x1)=f(0)= >0=x1,y2=f(y1)=f(
>0=x1,y2=f(y1)=f( )=
)= <
<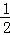 =y1,
=y1,
綜上,x1<x2<x0<y2<y1.
用數學歸納法證明如下:
①當n=1時,上面已證明成立.
②假設當n=k(k≥1)時有xk<xk+1<x0<yk+1<yk.
當n=k+1時,
由f(x)是單調增函數,有f(xk)<f(xk+1)<f(x0)<f(yk+1)<f(yk),
∴xk+1<xk+2<x0<yk+2<yk+1
由①②知對一切n=1,2,都有xn<xn+1<x0<yn+1<yn.
(3)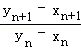 =
= =yn2+xnyn+xn2﹣(yn+xn)+
=yn2+xnyn+xn2﹣(yn+xn)+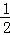 ≤(yn+xn)2﹣(yn+xn)+
≤(yn+xn)2﹣(yn+xn)+
=[(yn+xn)﹣ ]2+
]2+ .
.
由(Ⅱ)知0<yn+xn<1.
∴﹣ <yn+xn﹣
<yn+xn﹣ <
< ,
,
∴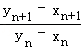 <(
<( )2+
)2+ =
=


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:高中數學 來源:[同步]2015年北師大版選修1-1 3.3計算導數練習卷(解析版) 題型:選擇題
y=sinx(cosx+1)的導數是( )
A.cos2x﹣cosx B.cos2x+cosx
C.cos2x+sinx D.cos2x+cosx
查看答案和解析>>
科目:高中數學 來源:[同步]2015年北師大版必修一 3.1 正整數指數函數練習卷(解析版) 題型:解答題
已知集合A={m|正整數指數函數y=(m2+m+1)•( )x,x∈N+},求集合A.
)x,x∈N+},求集合A.
查看答案和解析>>
科目:高中數學 來源:[同步]2015年北師大版必修一 2.1 生活中的變量關系練習卷(解析版) 題型:填空題
在某報《自測健康狀況》的報道中,自測血壓結果與相應年齡的統計數據如下表.觀察表中數據的特點,用適當的數填入表中空白( )內.
年齡(歲) | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 |
收縮壓(水銀柱 毫米) | 110 | 115 | 120 | 125 | 130 | 135 | ( ) | 145 |
舒張壓(水銀柱 毫米) | 70 | 73 | 75 | 78 | 80 | 83 | ( ) | 88 |
查看答案和解析>>
科目:高中數學 來源:[同步]2015年北師大版必修一 2.1 生活中的變量關系練習卷(解析版) 題型:選擇題
變量x與變量y,w,z的對應關系如下表所示:
x | 1 | 2 | 3 | 1 | 5 | 6 |
y | -1 | -2 | -3 | -4 | -1 | -6 |
w | 2 | 0 | 1 | 2 | 4 | 8 |
z | 0 | 0 | 0 | 0 | 0 | 0 |
下列說法正確的是( )
A.y是x的函數 B.w不是x的函數 C.z是x的函數 D.z不是x的函數
查看答案和解析>>
科目:高中數學 來源:[同步]2015年人教B版選修4-5 3.1 數學歸納法原理練習卷(解析版) 題型:選擇題
在數學歸納法證明多邊形內角和定理時,第一步應驗證( )
A.n=1成立 B.n=2成立 C.n=3成立 D.n=4成立
查看答案和解析>>
科目:高中數學 來源:[同步]2015年人教B版選修1-2 1.2回歸分析練習卷(解析版) 題型:選擇題
已知回歸直線的斜率的估計值為1.23,樣本點的中心為(4,5),則回歸直線方程為( )
A.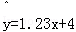 B.
B.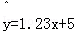 C.
C.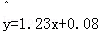 D.
D. =0.08x+1.23
=0.08x+1.23
查看答案和解析>>
科目:高中數學 來源:[同步]2015年人教A版選修1-1 3.4生活中的優化問題舉例練習卷(解析版) 題型:解答題
某種產品每件成本為6元,每件售價為x元(x>6),年銷量為u萬件,若已知 與
與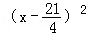 成正比,且售價為10元時,年銷量為28萬件.
成正比,且售價為10元時,年銷量為28萬件.
(1)求年銷售利潤y關于x的函數關系式.
(2)求售價為多少時,年利潤最大,并求出最大年利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com