Question

【題目】如圖半圓柱OO1的底面半徑和高都是1，面ABB1A1是它的軸截面（過上下底面圓心連線OO1的平面），Q，P分別是上下底面半圓周上一點．
（1）證明：三棱錐Q﹣ABP體積VQ﹣ABP≤ ，并指出P和Q滿足什么條件時有AP⊥BQ
（2）求二面角P﹣AB﹣Q平面角的取值范圍，并說明理由．

Answer 1

【答案】
（1）證明：VQ﹣ABP= ，其中h是Q到平面ABP的距離，（由條件及圓柱性質）即平面A1B1Q到ABP的距離且為定值1

由半圓性質∠APB=90°，所以AP2+BP2=4

所以由均值不等式s△ABP= ．

∴VQ﹣ABP= ≤

因為AP⊥PB，要有AP⊥BQ，只需要PQ⊥PA即可！

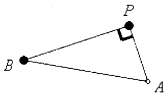
（2）解：

如圖以O為原點、OA為x軸、OO1為z軸建坐標系作QN垂直于平面ABP于N，

記∠AON=θ，θ∈[0，π]

A（1，O，O），B（﹣1，0，0），Q（cosθ，sinθ，0）

平面PAB法向量可取

設平面ABQ的法向量 ， ，

由 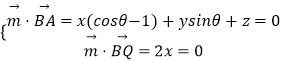，可取

∴θ∈（0， ]時，|cos＜ ， ＞|=

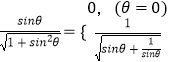
θ∈（0， ]時，sinθ+ ≥2．（當sinθ=1時取等號）

|cos＜ ， ＞|∈[0， ]，

所以二面角P﹣AB﹣Q平面角的取值范圍是：[ ， ]

【解析】（1）由條件及圓柱性質知平面A1B1Q到ABP的距離且為定值1，由半圓性質∠APB=90°，所以AP2+BP2=4 所以由均值不等式s△ABP= ．得VQ﹣ABP= ≤
由AP⊥PB可知，要有AP⊥BQ，只需要PQ⊥PA即可（2）以O為原點、OA為x軸、OO1為z軸建坐標系作QN垂直于平面ABP于N，記∠AON=θ，θ∈[0，π]，A（1，O，O），B（﹣1，0，0），Q（cosθ，sinθ，0）
平面PAB法向量可取
設平面ABQ的法向量 ，可取
θ∈（0， ]時，|cos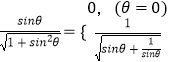＜ ， ＞|= 即可求二面角P﹣AB﹣Q平面角的取值范圍