
中國航母“遼寧艦”是中國第一艘航母,“遼寧”號以4臺蒸汽輪機為動力,為保證航母的動力安全性,科學家對蒸汽輪機進行了170余項技術改進,增加了某項新技術,該項新技術要進入試用階段前必須對其中的三項不同指標甲、乙、丙進行通過量化檢測。假如該項新技術的指標甲、乙、丙獨立通過檢測合格的概率分別為 、
、 、
、 。指標甲、乙、丙合格分別記為4分、2分、4分;若某項指標不合格,則該項指標記0分,各項指標檢測結果互不影響。
。指標甲、乙、丙合格分別記為4分、2分、4分;若某項指標不合格,則該項指標記0分,各項指標檢測結果互不影響。
(I)求該項技術量化得分不低于8分的概率;
(II)記該項新技術的三個指標中被檢測合格的指標個數為隨機變量X,求X的分布列與數學期望。
(1)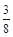 (II)分布列詳見解析;
(II)分布列詳見解析;
解析試題分析:(I) 記甲、乙、丙獨立通過檢測合格分別為事件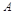 、
、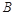 、
、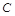 ,則
,則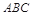 +
+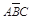 為得分不低于8分事件,然后根據互斥事件和獨立事件的概率公式求解即可.(II)寫出三個指標中被檢測合格的指標個數為隨機變量X的所有可能取值,然后計算相應的概率,列表記得分布列,最后根據數學期望公式求得期望值.
為得分不低于8分事件,然后根據互斥事件和獨立事件的概率公式求解即可.(II)寫出三個指標中被檢測合格的指標個數為隨機變量X的所有可能取值,然后計算相應的概率,列表記得分布列,最后根據數學期望公式求得期望值.
試題解析:解:(Ⅰ)該項新技術的三項不同指標甲、乙、丙獨立通過檢測合格分別為事件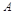 、
、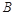 、
、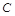 , 則事件“得分不低于8分”表示為
, 則事件“得分不低于8分”表示為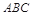 +
+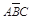 .
. 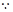
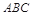 與
與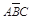 為互斥事件,且
為互斥事件,且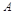 、
、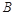 、
、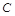 為彼此獨立
為彼此獨立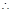
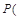
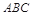 +
+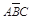
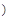 =
=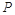 (
(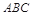 )+
)+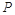 (
(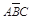 )
)
=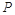 (
(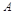 )
)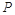 (
(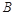 )
)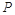 (
(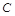 )+
)+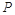 (
(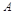 )
)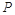 (
( )
)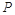 (
(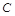 )=
)=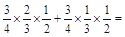
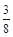 5分
5分
(Ⅱ)該項新技術的三個指標中被檢測合格的指標個數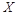 的取值為0,1,2,3. 6分
的取值為0,1,2,3. 6分
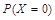 =
=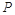 (
(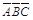 )=
)=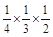 =
=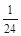 ,
, 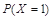 =
=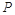 (
(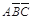 +
+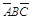 +
+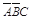 )=
)=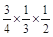 +
+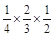 +
+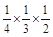 =
=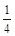 ,
, 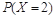 =
=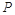 (
(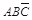 +
+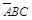 +
+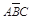 )=
)=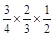 +
+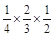 +
+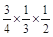 =
=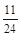 ,
, 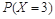 =
=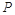 (
(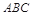 )=
)=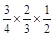 =
=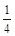 , 10分
, 10分
隨機變量

 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案科目:高中數學 來源: 題型:解答題
為了了解某市工廠開展群眾體育活動的情況,擬采用分層抽樣的方法從 三個區中抽取6個工廠進行調查.已知
三個區中抽取6個工廠進行調查.已知 區中分別有27,18,9個工廠.
區中分別有27,18,9個工廠.
(Ⅰ)求從 區中應分別抽取的工廠個數;
區中應分別抽取的工廠個數;
(Ⅱ)若從抽得的6個工廠中隨機地抽取2個進行調查結果的對比,求這2個工廠中至少有1個來自 區的概率.
區的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了調查學生的視力情況,隨機抽查了一部分學生的視力,將調查結果分組,分組區間為 ,經過數據處理,得到如下頻率分布表
,經過數據處理,得到如下頻率分布表
| 分組 | 頻數 | 頻率 |
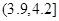 | 3 | 0.06 |
 | 6 | 0.12 |
 | 25 | 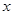 |
 | 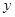 | 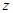 |
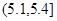 | 2 | 0.04 |
| 合計 | 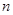 | 1.00 |
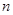 ,
,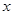 ,
,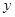 ,
,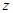 的值
的值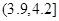 和
和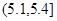 的所有同學中隨機抽取兩人,求兩人視力差的絕對值低于
的所有同學中隨機抽取兩人,求兩人視力差的絕對值低于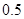 的概率
的概率查看答案和解析>>
科目:高中數學 來源: 題型:解答題
電子蛙跳游戲是:青蛙第一步從如圖所示的正方體 頂點
頂點 起跳,每步從一頂點跳到相鄰的頂點.
起跳,每步從一頂點跳到相鄰的頂點.
(1)求跳三步跳到 的概率
的概率 ;
;
(2)青蛙跳五步,用 表示跳到過
表示跳到過 的次數,求隨機變量
的次數,求隨機變量 的概率分布及數學期望
的概率分布及數學期望 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
下圖是某市3月1日至14日的空氣質量指數趨勢圖,空氣質量指數小于100表示空氣質量優良,空氣質量指數大于200表示空氣重度污染,某人隨機選擇3月1日至3月13日中的某一天到達該市,并停留2天.
(Ⅰ)求此人到達當日空氣重度污染的概率;
(Ⅱ)設X是此人停留期間空氣質量優良的天數,求X的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
用分層抽樣方法從高中三個年級的相關人員中抽取若干人組成研究小組,有關數據見下表:(單位:人)
(Ⅰ)求 ,
,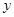 ;
;
(Ⅱ)若從高二、高三年級抽取的人中選 人,求這2人都來自高二年級的概率.
人,求這2人都來自高二年級的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某小組共有 、
、 、
、 、
、 、
、 五位同學,他們的身高(單位:米)以及體重指
五位同學,他們的身高(單位:米)以及體重指
標(單位:千克/米2)如下表所示:
| |  |  |  |  |  |
| 身高 |  |  |  |  |  |
| 體重指標 |  |  |  |  |  |
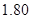 的同學中任選
的同學中任選 人,求選到的
人,求選到的 人身高都在
人身高都在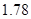 以下的概率;
以下的概率; 人,求選到的
人,求選到的 人的身高都在
人的身高都在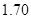 以上且體重指標都在
以上且體重指標都在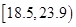 中的概率.
中的概率.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
其市有小型超市72個,中型超市24個,大型超市12個,現采用分層抽樣方法抽取9個超市對其銷售商品質量進行調查.
(I)求應從小型、中型、大型超市分別抽取的個數;
(II)若從抽取的9個超市中隨機抽取3個做進一步跟蹤分析,記隨機變量X為抽取的小型超市的個數,求隨機變量X的分布列及數學期望E(X) .
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某學生參加某高校的自主招生考試,須依次參加A,B,C,D,E五項考試,如果前四項中有兩項不合格或第五項不合格,則該考生就被淘汰,考試即結束;考生未被淘汰時,一定繼續參加后面的考試.已知每一項測試都是相互獨立的,該生參加A,B,C,D四項考試不合格的概率均為 ,參加第五項不合格的概率為
,參加第五項不合格的概率為 .
.
(1)求該生被錄取的概率;
(2)記該生參加考試的項數為X,求X的分布列和期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com